bitmap 算法

Intro to RoaringBitmap | Every bit matters!

高性能bitmap的实现

Posted by Wang Junwei on 2023-12-13
Intro to RoaringBitmap | Every bit matters!

本文首发于个人博客 : 🔗Wang Junwei’s Blog :Intro to RoaringBitmap | Every bit matters!

前言

最开始学到这个单词的时候，还是19年秋选修《计算机视觉》、《计算机图形学》的时候，那个时候连想起来的中文词语含义还是点阵图像，比如 BMP格式的图片文件，这里的bit是颜色深度，越深表示颜色分辨率越好，图片显示效果越好。比如我们常见的RGB的Hex颜色表示法，0xff00ff就是紫色。

img

这次的主角是bitmap-index/algorithm, 用bit位来进行海量规模记录/查询的数据结构。

秋招的时候简单了解过bitmap的实现，但从来没机会深入了解过底层细节，这几天在排查一个稳定性问题的时候遇到了bitmap操作bottleneck导致的pendingtask；借此机会，好好深入看一下CRoaring的源代码吧。

BitMap简介

位图（Bitmap）是一种用于表示集合的数据结构，其中每个元素用二进制位表示，适用于高效存储和查询元素的存在性。在内存结构中表现为用大量的0、1来表示元素的存在性，一般用来过滤/去重。

简单实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Bitmap {
private:
    std::vector<uint32_t> bits;
public:
    // 构造函数，初始化位图
    Bitmap(size_t size) : bits((size + 31) / 32, 0) {}
    // 设置第i位
    void set(size_t i) {
        bits[i / 32] |= (1ull << (i % 32));
    }
    // 清除第i位
    void clear(size_t i) {
        bits[i / 32] &= ~(1ull << (i % 32));
    }
    // 获取第i位的值
    bool test(size_t i) const {
        return (bits[i / 32] & (1ull << (i % 32))) != 0;
    }
};

假设我们有 10 亿个不同的元素，要对这些元素的存在性进行存储。如果使用传统的数据结构（如数组或散列表），每个元素需要一个独立的存储单元，这可能占据很大的内存空间。

如果用int32_t数组来存储，大概需要

1,000,000,000×4B≈4×1024×1024×1024B=4×1024 MB=4 GB\begin{aligned} 1,000,000,000\times 4 B &\approx 4 \times 1024 \times 1024\times 1024 B \\ &= 4\times 1024 \space MB \\ &= 4\space GB \\ \end{aligned}

而使用 Bitmap，我们可以将这 10 亿个元素映射到一个二进制位图上，其中每个位表示一个元素的存在性。如果每个元素用一个位表示，那么我们只需要 10 亿 bits，或者约 119 MB 的内存空间。

1,000,000,000 b≈1024×1024×1024 b=1024 Mb=128 MB\begin{aligned} 1,000,000,000 \space b &\approx 1024\times 1024\times 1024\space b \\ &= 1024\space Mb \\ &= 128\space MB \\ \end{aligned}

这个比较仅仅是一个示例，实际情况中具体的存储大小可能会受到数据分布的影响。

比如，如果候选库很稀疏的话，比如只有{0, 1, 3, 800000000} 这四个元素，却需要 800000000/32* 4 = 100000000 个字节，大概需要100MB的内存空间来记录，太可怕了。

这个时候，就需要一些针对性的优化了，很多研究者提出了各种算法对稀疏位图进行压缩，减少内存占用并提高效率。比较有代表性的有WAH[1]、EWAH[2]、Concise[3]，以及本文要介绍的RoaringBitmap[4]，咆哮位图。（PS，咆哮哈哈哈）

RoaringBitmap

https://arxiv.org/pdf/1402.6407.pdf

https://arxiv.org/pdf/1709.07821.pdf

Overview

image-20231216133407697

RoaringBitmap的核心是分段处理。

bitmap要存储的一般都是int*类型的整数，uint32_t可以表征的范围是[0, 4294967295]，大约能存储43亿的数据，大于某电商的全库商品/某短视频的全部视频数量；一般情况是够用了。

Roaringbitmap 将int32分段处理，高16位当作container的index；低16位用来在具体的container中存储，二者组合起来就可以在bitmap对象中找到某个int32的值。把[0, 2^32) 的数据空间分段处理，表示为[0, 1<< 16)、[1<< 16, 2<<16)、[2<<16, 3 << 16) … 总共 1<<16个段——也就是高16位的索引范围。

另一个角度，可以把Roaringbitmap看作是一个std::list<uint16_t，Container> (数组元素是高16bit，2个字节的值)，每一个元素都是一个容器指针，这个容器指向一个16bit数据的集合（低16位）; 容器类型可以动态变化，根据每一个bucket的实时存储量来动态调节，来最大化利用内存空间。

roaringbitmap主要有三类container: Array Container, Run Container 和 Bitset Container.

roaring_bitmap_s

1
2
3
4
5
6
7
8
9
10
11
12
typedef struct roaring_array_s {
    int32_t size;
    int32_t allocation_size;
    void **containers;  // Use container_t in non-API files!
    uint16_t *keys;
    uint8_t *typecodes;
    uint8_t flags;
} roaring_array_t;

typedef struct roaring_bitmap_s {
    roaring_array_t high_low_container;
} roaring_bitmap_t;

  • keys

    为高16位的数组指针，在通过H16寻址容器指针的时候，也是通过二分查找实现

    1
    2
    3
    4
    inline int32_t ra_get_index(const roaring_array_t *ra, uint16_t x) {
        if ((ra->size == 0) || ra->keys[ra->size - 1] == x) return ra->size - 1;
        return binarySearch(ra->keys, (int32_t)ra->size, x);
    }

  • containers

    为此bitmap的指针数组，数组的大小和keys保持一致，而且可以外键对齐offset；

  • typecodes

    为container类型数组，数组大小和keys保持一致，typecodes[i] 表示H16 = keys[i]的bucket的容器类型，主要有以下几种

    • BITSET_CONTAINER_TYPE
    • ARRAY_CONTAINER_TYPE
    • RUN_CONTAINER_TYPE
    • SHARED_CONTAINER_TYPE

Array Container

1
2
3
4
5
struct array_container_s {
    int32_t cardinality;		//容器中有效的indices的数量
    int32_t capacity;				//容器已经申请过的size，表示容量
    uint16_t *array;
};

顾名思义，Array Container 存储的是一个array<uint16_t>数组，未来快速查询/插入，array被设计成一个有序数组，在添加元素或者删除元素的时候，都需要维持顺序，可以通过二分查找(binary search) 加速。

有如下特性

  • element的类型都是unsigned short int 2个Byte.
  • container的容量是**[4,4096)**
    • 当插入元素超过4096的时候，array container会被动态转换为Bitset Container
1
2
3
4
5
6
7
/**
 * Get the index corresponding to a 16-bit key
 */
inline int32_t ra_get_index(const roaring_array_t *ra, uint16_t x) {
    if ((ra->size == 0) || ra->keys[ra->size - 1] == x) return ra->size - 1;
    return binarySearch(ra->keys, (int32_t)ra->size, x);
}

以131090插入为例，其H16位为 0000 0000 0000 0010 = 2，L16 位为 0000 0000 0001 0010 = 10这个bucket会指向一个array_container_s的对象，在array_container_s.array中二分查找10，查看其是否存在，不存在的话，返回第一个不大于10的元素的index；然后在这个位置执行插入

img

array_container_try_add

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Add value to the set if final cardinality doesn't exceed max_cardinality.
 * Return code:
 * 1  -- value was added
 * 0  -- value was already present
 * -1 -- value was not added because cardinality would exceed max_cardinality
 */
static inline int array_container_try_add(array_container_t *arr, uint16_t value,
                                          int32_t max_cardinality) {
    const int32_t cardinality = arr->cardinality;

    // best case, we can append.
    if ((array_container_empty(arr) || arr->array[cardinality - 1] < value) &&
        cardinality < max_cardinality) {
        array_container_append(arr, value);
        return 1;
    }
  
  	// 二分查找 loc
    const int32_t loc = binarySearch(arr->array, cardinality, value);

    if (loc >= 0) {
        return 0;
    } else if (cardinality < max_cardinality) {
        if (array_container_full(arr)) {
            array_container_grow(arr, arr->capacity + 1, true);
        }
        const int32_t insert_idx = -loc - 1;
        memmove(arr->array + insert_idx + 1, arr->array + insert_idx,
                (cardinality - insert_idx) * sizeof(uint16_t));
        arr->array[insert_idx] = value;
        arr->cardinality++;
        return 1;
    } else {
        return -1;
    }
}

这段代码很容易理解：

  1. 首先如果 容器为空、容器最大值小于要插入的值value（low 16-bit），直接在最后插入。

  2. 二分查找元素 value，返回index offset 为 loc；

    1. loc >= 0 表示已经有这个元素了，直接返回

    2. cardinality >= max_cardinality 表示当前容器满了，返回-1，在后续逻辑中会动态转化为bitset container.

    3. 在容器没超过上限的的情况下 检查容器是否已经满; ⚠️注意，这里的满指的是已经申请的空间是不是完全用完了，而不是是否超过4096，如果是用完了，就需要扩容；

      1
      2
      3
      static inline bool array_container_full(const array_container_t *array) {
          return array->cardinality == array->capacity;
      }

    4. 将[insert_idx, end] 的元素整体向后移动一位memmove 然后插入当前值。

BitSet Container

bitset 容器则是一个经典的bitmap实现，真正的做到了用每一个bit来表征一个值的存在。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct bitset_container_s {
    int32_t cardinality;
    uint64_t *words;
};

enum {
    BITSET_CONTAINER_SIZE_IN_WORDS = (1 << 16) / 64,
    BITSET_UNKNOWN_CARDINALITY = -1
};

bitset_container_t *bitset_container_create(void) {
    bitset_container_t *bitset =
        (bitset_container_t *)roaring_malloc(sizeof(bitset_container_t));
  
    if (!bitset) {
        return NULL;
    }
    size_t align_size = 32;
  
    bitset->words = (uint64_t *)roaring_aligned_malloc(
        align_size, sizeof(uint64_t) * BITSET_CONTAINER_SIZE_IN_WORDS);
    if (!bitset->words) {
        roaring_free(bitset);
        return NULL;
    }
    bitset_container_clear(bitset);
    return bitset;
}
  • cardinality 表示当前的元素总量。
  • words 是一段内存空间，用来存储[0, 1<<16)数据，每一个数据需要一个bit，所以大小固定为 1 << 16 / 64 个 uint64_t的空间。

以插入32786（高H16 = 0000 0000 0000 0000，低L16 = 1000 0000 0001 0010）为例，在第0个类型为BitMap Container的容器中，查找第1000 0000 0001 0010个bit是否为0/1.

bitset_container_add

1
2
3
4
5
6
7
8
9
10
11
12
/* Add `pos' to `bitset'. Returns true if `pos' was not present. Might be slower
 * than bitset_container_set.  */
static inline bool bitset_container_add(bitset_container_t *bitset,
                                        uint16_t pos) {
    const uint64_t old_word = bitset->words[pos >> 6];
    const int index = pos & 63;
    const uint64_t new_word = old_word | (UINT64_C(1) << index);
    const uint64_t increment = (old_word ^ new_word) >> index;
    bitset->cardinality += (uint32_t)increment;
    bitset->words[pos >> 6] = new_word;
    return increment > 0;
}

这段代码里面写的有点简略，这里面的6，63 都没有解释，最好用个宏定义起来，比如:

1
2
#define UINT64_T_ARRAY_BIT_INDEX 6
#define UINT64_T_MASK 0x3f  /*63 = (0011 1111)*/
  • old_word 是pos对应的bit所在的qword
  • index 表示pos在old_word里面的第index个bit上
  • new_word = old_word | (UINT64_C(1) << index); 把第pos个bit置1
  • increment 用到了异或运算来快速找到从old_word到new_word是否有变化
    • increment > 0 表示之前pos不存在于pos里面，return true
    • increment 表示第pos个bit在add之前就已经是1了，无需操作return false

Run Container

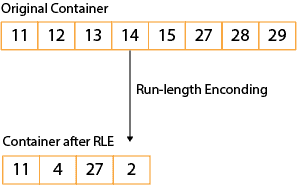
Run Container 是一个经典的Run-Length Encoding(RLE, 行程长度编码)设计。

它的主要思想是将连续的整数序列表示为一个 “run”，其中包含起始值和长度，比如[0,99)。这种编码方式可以显著减小存储空间，特别适用于表示连续的整数序列。在array container 或者 bitset container中有大量idle word的时候（稀疏），RLE container或许是一个很好的选项。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct run_container_s {
    int32_t n_runs;
    int32_t capacity;
    rle16_t *runs;
};

typedef struct rle16_s {
    uint16_t value;
    uint16_t length;
} rle16_t;

/* Create a new run container. Return NULL in case of failure. */
run_container_t *run_container_create_given_capacity(int32_t size) {
    run_container_t *run;
    /* Allocate the run container itself. */
    if ((run = (run_container_t *)roaring_malloc(sizeof(run_container_t))) == NULL) {
        return NULL;
    }
    if (size <= 0 ) { // we don't want to rely on malloc(0)
        run->runs = NULL;
    } else if ((run->runs = (rle16_t *)roaring_malloc(sizeof(rle16_t) * size)) == NULL) {
        roaring_free(run);
        return NULL;
    }
    run->capacity = size;
    run->n_runs = 0;
    return run;
}

RLE Container

  • rle16_s 表示run的offset 和 length，表达了一个[value, vlaue + length - 1]的一个闭区间

    • rle16_s::value 是一个区间的起点偏移offset
    • rle16_s::length是这个区间的长度

  • capacity 表示所有区间的长度和，即所有元素的总数

run_container_add

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
bool run_container_add(run_container_t *run, uint16_t pos) {
    int32_t index = interleavedBinarySearch(run->runs, run->n_runs, pos);
    if (index >= 0) return false;  // already there
    index = -index - 2;            // points to preceding value, possibly -1
    if (index >= 0) {              // possible match
        int32_t offset = pos - run->runs[index].value;
        int32_t le = run->runs[index].length;
        if (offset <= le) return false;  // already there
        if (offset == le + 1) {
            // we may need to fuse
            if (index + 1 < run->n_runs) {
                if (run->runs[index + 1].value == pos + 1) {
                    // indeed fusion is needed
                    run->runs[index].length = run->runs[index + 1].value +
                                              run->runs[index + 1].length -
                                              run->runs[index].value;
                    recoverRoomAtIndex(run, (uint16_t)(index + 1));
                    return true;
                }
            }
            run->runs[index].length++;
            return true;
        }
        if (index + 1 < run->n_runs) {
            // we may need to fuse
            if (run->runs[index + 1].value == pos + 1) {
                // indeed fusion is needed
                run->runs[index + 1].value = pos;
                run->runs[index + 1].length = run->runs[index + 1].length + 1;
                return true;
            }
        }
    }
    if (index == -1) {
        // we may need to extend the first run
        if (0 < run->n_runs) {
            if (run->runs[0].value == pos + 1) {
                run->runs[0].length++;
                run->runs[0].value--;
                return true;
            }
        }
    }
    makeRoomAtIndex(run, (uint16_t)(index + 1));
    run->runs[index + 1].value = pos;
    run->runs[index + 1].length = 0;
    return true;
}

Run Container的查找和插入稍微复杂一点，涉及区间数组和查找，增删合并。很久很久之前在秋招的时候经常刷到这种面试题

56. 合并区间

1288. 删除被覆盖区间

  1. int32_t index = interleavedBinarySearch(run->runs, run->n_runs, pos);：通过二分查找（interleaved binary search）找到整数 pos 在 Run Container 中的位置。如果找到了，index 的值将是非负的，表示找到了匹配的值；如果没有找到，index 的值将是负的，表示没找到但是插入位置已经确定。

    • Interleaved binary search

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      inline int32_t interleavedBinarySearch(const rle16_t *array, int32_t lenarray,
                                             uint16_t ikey) {
          int32_t low = 0;
          int32_t high = lenarray - 1;
          while (low <= high) {
              int32_t middleIndex = (low + high) >> 1;
              uint16_t middleValue = array[middleIndex].value;
              if (middleValue < ikey) {
                  low = middleIndex + 1;
              } else if (middleValue > ikey) {
                  high = middleIndex - 1;
              } else {
                  return middleIndex;
              }
          }
          return -(low + 1);
      }

  2. if (index >= 0) return false;：如果 pos 已经存在于 Run Container 中，则直接返回 false，因为不需要重复添加。

  3. index = -index - 2;：将负的 index 转换为插入位置的索引，准备进行后续的插入。

  4. if (index >= 0)：如果找到了插入位置，进一步判断是否有可能进行合并（fuse）。

    a. 如果 offset <= le，表示 pos 已经存在于当前行程（run）中，无需添加，返回 false。

    b. 如果 offset == le + 1，表示 pos 与当前行程相邻，可能需要合并。进行相应的合并操作。

    c. 如果以上条件不满足，检查是否需要与下一个行程进行合并。

  5. 如果 index == -1：表示 pos 为第一个元素，检查是否可以与第一个行程进行合并。

  6. 如果上述条件都不满足，说明需要插入一个新的行程。调用 makeRoomAtIndex 函数为新行程腾出空间，并将新的行程信息添加到 Run Container 中。

Operators

bitmap支持并、交、差集等基本集合运算；典型的，以bitset为例：

Bitset::operators

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
BITSET_CONTAINER_FN(or,    |, _mm256_or_si256, vorrq_u64)
BITSET_CONTAINER_FN(union, |, _mm256_or_si256, vorrq_u64)
BITSET_CONTAINER_FN(intersection, &, _mm256_and_si256, vandq_u64)
BITSET_CONTAINER_FN(xor,    ^,  _mm256_xor_si256,    veorq_u64)
BITSET_CONTAINER_FN(andnot, &~, _mm256_andnot_si256, vbicq_u64)
  
#define BITSET_CONTAINER_FN(opname, opsymbol, avx_intrinsic, neon_intrinsic)  \
int bitset_container_##opname(const bitset_container_t *src_1,            \
                              const bitset_container_t *src_2,            \
                              bitset_container_t *dst) {                  \
    const uint64_t * __restrict__ words_1 = src_1->words;                 \
    const uint64_t * __restrict__ words_2 = src_2->words;                 \
    uint64_t *out = dst->words;                                           \
    int32_t sum = 0;                                                      \
    for (size_t i = 0; i < BITSET_CONTAINER_SIZE_IN_WORDS; i += 2) {      \
        const uint64_t word_1 = (words_1[i])opsymbol(words_2[i]),         \
                       word_2 = (words_1[i + 1])opsymbol(words_2[i + 1]); \
        out[i] = word_1;                                                  \
        out[i + 1] = word_2;                                              \
        sum += roaring_hamming(word_1);                                    \
        sum += roaring_hamming(word_2);                                    \
    }                                                                     \
    dst->cardinality = sum;                                               \
    return dst->cardinality;                                              \
}

在CRoaring的代码中，用到了大量的SIMD指令集来加速bitset的求交集、求并集等基础操作, 如下

Intel® Intrinsics Guide https://www.intel.com/content/www/us/en/docs/intrinsics-guide/index.html#

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#if CROARING_COMPILER_SUPPORTS_AVX512
#define BITSET_CONTAINER_FN(opname, opsymbol, avx_intrinsic, neon_intrinsic)   \
  int bitset_container_##opname(const bitset_container_t *src_1,               \
                                const bitset_container_t *src_2,               \
                                bitset_container_t *dst) {                     \
    int support = croaring_hardware_support();                                 \
    if ( support & ROARING_SUPPORTS_AVX512 ) {                                 \
      return _avx512_bitset_container_##opname(src_1, src_2, dst);             \
    }                                                                          \
    else if ( support & ROARING_SUPPORTS_AVX2 ) {                              \
      return _avx2_bitset_container_##opname(src_1, src_2, dst);               \
    } else {                                                                   \
      return _scalar_bitset_container_##opname(src_1, src_2, dst);             \
    }                                                                          \
  }
  
#define AVX_BITSET_CONTAINER_FN2(before, opname, opsymbol, avx_intrinsic,               			\
                                neon_intrinsic, after)                                				\
  static inline int _avx2_bitset_container_##opname(const bitset_container_t *src_1,         	\
                                      const bitset_container_t *src_2,         \
                                      bitset_container_t *dst) {               \
    const __m256i *__restrict__ words_1 = (const __m256i *)src_1->words;       \
    const __m256i *__restrict__ words_2 = (const __m256i *)src_2->words;       \
    __m256i *out = (__m256i *)dst->words;                                      \
    dst->cardinality = (int32_t)avx2_harley_seal_popcount256andstore_##opname( \
        words_2, words_1, out,                                                 \
        BITSET_CONTAINER_SIZE_IN_WORDS / (WORDS_IN_AVX2_REG));                 \
    return dst->cardinality;                                                   \
  }

bitset 的集合操作很简答，可以复用C/C++的位运算符，在intrinsics指令集里面，也有很好的支持，可以用一系列的宏定义避免代码重复。

union |

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
void array_container_union(const array_container_t *array_1,
                           const array_container_t *array_2,
                           array_container_t *out) {
    const int32_t card_1 = array_1->cardinality, card_2 = array_2->cardinality;
    const int32_t max_cardinality = card_1 + card_2;

    if (out->capacity < max_cardinality) {
      array_container_grow(out, max_cardinality, false);
    }
    out->cardinality = (int32_t)fast_union_uint16(array_1->array, card_1,
                                      array_2->array, card_2, out->array);
}

size_t union_uint16(const uint16_t *set_1, size_t size_1, const uint16_t *set_2,
                    size_t size_2, uint16_t *buffer) {
    size_t pos = 0, idx_1 = 0, idx_2 = 0;

    if (0 == size_2) {
        memmove(buffer, set_1, size_1 * sizeof(uint16_t));
        return size_1;
    }
    if (0 == size_1) {
        memmove(buffer, set_2, size_2 * sizeof(uint16_t));
        return size_2;
    }

    uint16_t val_1 = set_1[idx_1], val_2 = set_2[idx_2];

    while (true) {
        if (val_1 < val_2) {
            buffer[pos++] = val_1;
            ++idx_1;
            if (idx_1 >= size_1) break;
            val_1 = set_1[idx_1];
        } else if (val_2 < val_1) {
            buffer[pos++] = val_2;
            ++idx_2;
            if (idx_2 >= size_2) break;
            val_2 = set_2[idx_2];
        } else {
            buffer[pos++] = val_1;
            ++idx_1;
            ++idx_2;
            if (idx_1 >= size_1 || idx_2 >= size_2) break;
            val_1 = set_1[idx_1];
            val_2 = set_2[idx_2];
        }
    }

    if (idx_1 < size_1) {
        const size_t n_elems = size_1 - idx_1;
        memmove(buffer + pos, set_1 + idx_1, n_elems * sizeof(uint16_t));
        pos += n_elems;
    } else if (idx_2 < size_2) {
        const size_t n_elems = size_2 - idx_2;
        memmove(buffer + pos, set_2 + idx_2, n_elems * sizeof(uint16_t));
        pos += n_elems;
    }

    return pos;
}

Fast_union的实现可以看成是两个有序数组合并的问题，经典到不能再经典的面试题：88. 合并两个有序数组 这里不再赘述。

Intersection &

其实在这里，我不太想继续贴代码了，好多循环展开的优化，占用了大量篇幅。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
int32_t intersect_skewed_uint16(const uint16_t *small, size_t size_s,
                                         const uint16_t *large, size_t size_l,
                                         uint16_t *buffer) {
  size_t pos = 0, idx_l = 0, idx_s = 0;

  if (0 == size_s) {
    return 0;
  }
  int32_t index1 = 0, index2 = 0, index3 = 0, index4 = 0;
  while ((idx_s + 4 <= size_s) && (idx_l < size_l)) {
    uint16_t target1 = small[idx_s];
    uint16_t target2 = small[idx_s + 1];
    uint16_t target3 = small[idx_s + 2];
    uint16_t target4 = small[idx_s + 3];
    binarySearch4(large + idx_l, (int32_t)(size_l - idx_l), target1, target2, target3,
                  target4, &index1, &index2, &index3, &index4);
    if ((index1 + idx_l < size_l) && (large[idx_l + index1] == target1)) {
      buffer[pos++] = target1;
    }
    if ((index2 + idx_l < size_l) && (large[idx_l + index2] == target2)) {
      buffer[pos++] = target2;
    }
    if ((index3 + idx_l < size_l) && (large[idx_l + index3] == target3)) {
      buffer[pos++] = target3;
    }
    if ((index4 + idx_l < size_l) && (large[idx_l + index4] == target4)) {
      buffer[pos++] = target4;
    }
    idx_s += 4;
    idx_l += index4;
  }
  if ((idx_s + 2 <= size_s) && (idx_l < size_l)) {
    uint16_t target1 = small[idx_s];
    uint16_t target2 = small[idx_s + 1];
    binarySearch2(large + idx_l, (int32_t)(size_l - idx_l), target1, target2, &index1,
                  &index2);
    if ((index1 + idx_l < size_l) && (large[idx_l + index1] == target1)) {
      buffer[pos++] = target1;
    }
    if ((index2 + idx_l < size_l) && (large[idx_l + index2] == target2)) {
      buffer[pos++] = target2;
    }
    idx_s += 2;
    idx_l += index2;
  }
  if ((idx_s < size_s) && (idx_l < size_l)) {
    uint16_t val_s = small[idx_s];
    int32_t index = binarySearch(large + idx_l, (int32_t)(size_l - idx_l), val_s);
    if (index >= 0)
      buffer[pos++] = val_s;
  }
  return (int32_t)pos;
}

比较值得一看的是 binaryseach4， binarysearch2 和binary_search的过程，有点意思

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
static void binarySearch4(const uint16_t *array, int32_t n, uint16_t target1,
                   uint16_t target2, uint16_t target3, uint16_t target4,
                   int32_t *index1, int32_t *index2, int32_t *index3,
                   int32_t *index4) {
  const uint16_t *base1 = array;
  const uint16_t *base2 = array;
  const uint16_t *base3 = array;
  const uint16_t *base4 = array;
  if (n == 0)
    return;
  while (n > 1) {
    int32_t half = n >> 1;
    base1 = (base1[half] < target1) ? &base1[half] : base1;
    base2 = (base2[half] < target2) ? &base2[half] : base2;
    base3 = (base3[half] < target3) ? &base3[half] : base3;
    base4 = (base4[half] < target4) ? &base4[half] : base4;
    n -= half;
  }
  *index1 = (int32_t)((*base1 < target1) + base1 - array);
  *index2 = (int32_t)((*base2 < target2) + base2 - array);
  *index3 = (int32_t)((*base3 < target3) + base3 - array);
  *index4 = (int32_t)((*base4 < target4) + base4 - array);
}

Difference &~

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
void run_container_andnot(const run_container_t *src_1,
                          const run_container_t *src_2, run_container_t *dst) {
    // following Java implementation as of June 2016

    if (dst->capacity < src_1->n_runs + src_2->n_runs)
        run_container_grow(dst, src_1->n_runs + src_2->n_runs, false);

    dst->n_runs = 0;

    int rlepos1 = 0;
    int rlepos2 = 0;
    int32_t start = src_1->runs[rlepos1].value;
    int32_t end = start + src_1->runs[rlepos1].length + 1;
    int32_t start2 = src_2->runs[rlepos2].value;
    int32_t end2 = start2 + src_2->runs[rlepos2].length + 1;

    while ((rlepos1 < src_1->n_runs) && (rlepos2 < src_2->n_runs)) {
        if (end <= start2) {
            // output the first run
            dst->runs[dst->n_runs++] = MAKE_RLE16(start, end - start - 1);
            rlepos1++;
            if (rlepos1 < src_1->n_runs) {
                start = src_1->runs[rlepos1].value;
                end = start + src_1->runs[rlepos1].length + 1;
            }
        } else if (end2 <= start) {
            // exit the second run
            rlepos2++;
            if (rlepos2 < src_2->n_runs) {
                start2 = src_2->runs[rlepos2].value;
                end2 = start2 + src_2->runs[rlepos2].length + 1;
            }
        } else {
            if (start < start2) {
                dst->runs[dst->n_runs++] =
                    MAKE_RLE16(start, start2 - start - 1);
            }
            if (end2 < end) {
                start = end2;
            } else {
                rlepos1++;
                if (rlepos1 < src_1->n_runs) {
                    start = src_1->runs[rlepos1].value;
                    end = start + src_1->runs[rlepos1].length + 1;
                }
            }
        }
    }
    if (rlepos1 < src_1->n_runs) {
        dst->runs[dst->n_runs++] = MAKE_RLE16(start, end - start - 1);
        rlepos1++;
        if (rlepos1 < src_1->n_runs) {
            memcpy(dst->runs + dst->n_runs, src_1->runs + rlepos1,
                   sizeof(rle16_t) * (src_1->n_runs - rlepos1));
            dst->n_runs += src_1->n_runs - rlepos1;
        }
    }
}
  1. if (dst->capacity < src_1->n_runs + src_2->n_runs)：如果 dst 的容量不足以容纳两个输入 Run Container 的所有行程（runs），则调用 run_container_grow 函数来扩展 dst 的容量。
  2. dst->n_runs = 0;：初始化 dst 的行程数量为 0。
  3. 初始化一些变量，如 rlepos1、rlepos2、start、end、start2、end2，用于迭代两个输入 Run Container 的行程。
  4. 使用 while 循环迭代两个输入 Run Container 的行程，执行以下操作：
    • 如果 end 小于等于 start2，表示当前 src_1 的行程没有与 src_2 的行程重叠，将 src_1 的行程添加到 dst 中，然后更新相关变量。
    • 如果 end2 小于等于 start，表示当前 src_2 的行程在当前 src_1 的行程之前结束，更新 src_2 相关变量。
    • 如果当前 src_1 和 src_2 的行程有重叠，执行适当的合并和更新操作。
  5. 处理迭代结束后可能剩余的 src_1 的行程。
    • 如果 rlepos1 < src_1->n_runs，表示还有未处理的 src_1 行程，将其添加到 dst 中。
    • 将未处理的 src_1 行程复制到 dst 中。

XOR ^

img

仍然以array container为例吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int32_t xor_uint16(const uint16_t *array_1, int32_t card_1,
                   const uint16_t *array_2, int32_t card_2, uint16_t *out) {
    int32_t pos1 = 0, pos2 = 0, pos_out = 0;
    while (pos1 < card_1 && pos2 < card_2) {
        const uint16_t v1 = array_1[pos1];
        const uint16_t v2 = array_2[pos2];
        if (v1 == v2) {
            ++pos1;
            ++pos2;
            continue;
        }
        if (v1 < v2) {
            out[pos_out++] = v1;
            ++pos1;
        } else {
            out[pos_out++] = v2;
            ++pos2;
        }
    }
    if (pos1 < card_1) {
        const size_t n_elems = card_1 - pos1;
        memcpy(out + pos_out, array_1 + pos1, n_elems * sizeof(uint16_t));
        pos_out += (int32_t)n_elems;
    } else if (pos2 < card_2) {
        const size_t n_elems = card_2 - pos2;
        memcpy(out + pos_out, array_2 + pos2, n_elems * sizeof(uint16_t));
        pos_out += (int32_t)n_elems;
    }
    return pos_out;
}
  1. 初始化三个指针 pos1、pos2、pos_out 分别表示 array_1、array_2 和 out 的当前位置。
  2. 使用 while 循环迭代两个有序数组，执行以下操作：
    • 如果 array_1[pos1] 等于 array_2[pos2]，表示两个元素相同，将两个指针同时向后移动一位。
    • 如果 array_1[pos1] 小于 array_2[pos2]，表示 array_1 的当前元素较小，将其存储到 out 中，然后移动 array_1 的指针。
    • 如果 array_2[pos2] 小于 array_1[pos1]，表示 array_2 的当前元素较小，将其存储到 out 中，然后移动 array_2 的指针。
  3. 处理可能剩余的元素：
    • 如果 pos1 没有遍历完 array_1，将剩余的元素复制到 out 中。
    • 如果 pos2 没有遍历完 array_2，将剩余的元素复制到 out 中。
  4. 返回 pos_out，即存储结果的数组 out 的实际大小（元素数量）。

Container Switching.

1
2
3
4
5
6
bitset_container_t *bitset_container_from_array(const array_container_t *arr);
bitset_container_t *bitset_container_from_run(const run_container_t *arr);
array_container_t *array_container_from_run(const run_container_t *arr);
array_container_t *array_container_from_bitset(const bitset_container_t *bits);
run_container_t *run_container_from_array(const array_container_t *c);
//...

Array -> BitSet

当bitmap运行时，比如add了很多的数据导致array container的cardinality超过了4096的上限，会触发bitset_container_from_array的转换操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bitset_container_t *bitset_container_from_array(const array_container_t *ac) {
    bitset_container_t *ans = bitset_container_create();
    int limit = array_container_cardinality(ac);
    for (int i = 0; i < limit; ++i) bitset_container_set(ans, ac->array[i]);
    return ans;
}
static inline void bitset_container_set(bitset_container_t *bitset,
                                        uint16_t pos) {
    const uint64_t old_word = bitset->words[pos >> 6];
    const int index = pos & 63;
    const uint64_t new_word = old_word | (UINT64_C(1) << index);
    bitset->cardinality += (uint32_t)((old_word ^ new_word) >> index);
    bitset->words[pos >> 6] = new_word;
}

上述代码逻辑很简单，如下：

  1. alloc一个bitset_container_t ans，并获取当前需要转换的array_container_t ac 的cardinality
  2. 遍历这个container，把所有的元素在 ans 中对应的bit 置为1

Run -> BitSet

对于从run container的转换，逻辑其实也差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
static inline void bitset_set_lenrange(uint64_t *words, uint32_t start,
                                       uint32_t lenminusone) {
    uint32_t firstword = start >> 6;
    uint32_t endword = (start + lenminusone) >> 6;
    if (firstword == endword) {
        words[firstword] |= ((~UINT64_C(0)) >> ((63 - lenminusone) % 64))
                             << (start % 64);
        return;
    }
    uint64_t temp = words[endword];
    words[firstword] |= (~UINT64_C(0)) << (start % 64);
    for (uint32_t i = firstword + 1; i < endword; i += 2)
        words[i] = words[i + 1] = ~UINT64_C(0);
    words[endword] =
        temp | (~UINT64_C(0)) >> (((~start + 1) - lenminusone - 1) % 64);
}
  1. uint32_t firstword = start >> 6;：计算起始位置 start 对应的64位字数组中的索引。
  2. uint32_t endword = (start + lenminusone) >> 6;：计算范围结束位置对应的64位字数组中的索引。
  3. if (firstword == endword)：如果起始位置和结束位置在同一个64位字中，执行以下操作：
    • words[firstword] |= ((~UINT64_C(0)) >> ((63 - lenminusone) % 64)) << (start % 64);：将指定范围内的位设置为1。通过构造一个掩码，将指定长度的位设为1，然后将其左移以匹配起始位置，最后使用位或运算符将结果合并到相应的64位字中。
  4. 如果起始位置和结束位置不在同一个64位字中，执行以下操作：
    • uint64_t temp = words[endword];：保存结束位置对应的64位字，准备后续使用。
    • words[firstword] |= (~UINT64_C(0)) << (start % 64);：将起始位置对应的64位字中指定范围内的位设置为1。
    • for (uint32_t i = firstword + 1; i < endword; i += 2)：循环设置两个相邻64位字中的所有位为1。注意，这里使用了 i += 2 来跳过中间的64位字，因为它们将在下一步的操作中被处理。
    • words[endword] = temp | (~UINT64_C(0)) >> (((~start + 1) - lenminusone - 1) % 64);：将结束位置对应的64位字还原，然后将指定范围内的位设置为1。

Eneding

今天先写到这里吧，最近阅读了一些类似elastic search的DSL filter，将海量数据的业务过滤逻辑用bitmap描述清楚，在线服务的时候用 filter op来试试过滤；例如Must, MustNot, range greater,lesser等绑定在候选的某个属性上，在检索时过滤，等过段时间闲下来了再好好阅读分享一下吧，敬请期待。

Reference

  1. Wu K, Stockinger K, Shoshani A. Breaking the curse of cardinality on bitmap indexes. SSDBM’08, Springer: Berlin, Heidelberg, 2008; 348–365.
  2. Lemire D, Kaser O, Aouiche K. Sorting improves word-aligned bitmap indexes. Data & Knowledge Engineering 2010; 69(1):3–28, doi:10.1016/j.datak.2009.08.006.
  3. Colantonio A, Di Pietro R. Concise: Compressed ’n’ Composable Integer Set. Information Processing Letters 2010; 110(16):644–650, doi:10.1016/j.ipl.2010.05.018.
  4. Chambi S , Lemire D , Kaser O , et al. Better bitmap performance with Roaring bitmaps[J]. Software—practice & Experience, 2016, 46(5):709-719.
FEATURED TAGS
bitmap 算法
FRIENDS