LSQ量化感知训练

随着深度学习的广泛应用，对于模型的压缩和加速变得越来越重要。其中，模型参数量化是一种有效的压缩方法，通过将浮点数参数转换为整数，从而减少了模型的存储和计算开销。本文将介绍一种新的量化方法，即LSQ量化，它可以通过学习量化参数来优化量化误差，并在保持模型精度的同时，大大减少模型的存储和计算开销。

LSQ量化是一种基于梯度量化和误差反传的低比特量化方法，可以用来将深度神经网络中的权重和激活值量化为较低比特位数，从而减少模型大小、加速推理速度并降低模型能耗。在本篇博客中，我们将详细讲解LSQ量化的原理，包括量化误差的计算、梯度的反向传播以及具体的代码实现。

模型量化

在深度学习中，模型的参数通常是浮点数，其存储和计算开销较大。为了减少模型的存储和计算开销，可以将浮点数参数量化为整数。假设模型中的参数为w，量化函数为Q，那么量化后的参数为：

$$Q(w) = round(w/s)\times s$$

其中，$s$为量化因子，也称为量化步长。通过量化，可以将浮点数参数$w$转化为整数，从而减少了模型的存储和计算开销。

但是，由于量化会引入量化误差，即量化后的参数与原始浮点数参数之间的误差，因此需要在保持模型精度的前提下，尽可能减少量化误差。传统的量化方法通常使用固定的量化因子和量化函数，无法优化量化误差。为了解决这个问题，LSQ量化方法提出了一种新的量化方法，可以通过学习量化参数来优化量化误差

普通量化训练

在量化训练中需要加入伪量化节点 (Fake Quantize)，这些节点做的事情就是把输入的 float 数据量化一遍后，再反量化回 float，以此来模拟量化误差，同时在反向传播的时候，发挥 STE 的功能，把导数回传到前面的层。

Fake Quantize 的过程可以总结成以下公式 (为了方便讲解 LSQ，这里采用 LSQ 中的对称量化的方式)：

$$\begin{aligned} & \bar{v}=\operatorname{round}\left(\operatorname{clip}\left(v / s,-Q_N, Q_P\right)\right) \\ \end{aligned}$$

$$\begin{aligned} & \hat{v}=\bar{v} \times s \end{aligned}$$

其中, $v$ 是 float 的输入, $\bar{v}$ 是量化后的数据 (仍然使用 float 来存储, 但数值由于做了 round 操作, 因此是整数), $\hat{v}$ 是反量化的结果。 $-Q_N$ 和 $Q_P$ 分别是 量化数值的最小值和最大值 (在对称量化中, $Q_N 、 Q_P$ 通常是相等的), $s$ 是量化参数。
由于 round 操作会带来误差, 因此 $\hat{v}$ 和 $v$ 之间存在量化误差, 这些误差反应到 loss 上会产生梯度, 这样就可以反向传播进行学习。每次更新 weight 后, 我 们会得到新的 float 的数值范围, 然后重新估计量化参数 $s$ :

$$s=\frac{|v|_{\max }}{Q_P}$$

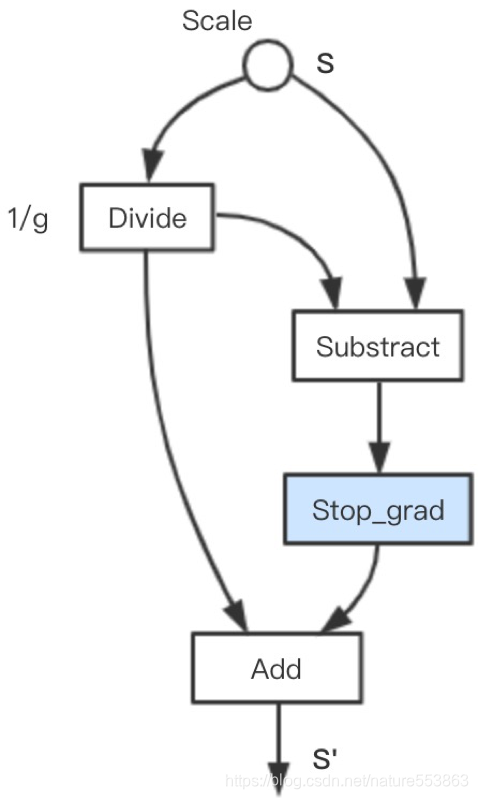
接着进入下一轮训练

LSQ量化的原理

Forward:

$$s^{\prime}=\frac{s}{g}+\text { stop\_grad }\left(s-\frac{s}{g}\right)$$

Backward:

$$\frac{\partial L}{\partial s}=\frac{\partial L}{\partial s^{\prime}} \frac{\partial s^{\prime}}{\partial s}=\frac{1}{g} \frac{\partial L}{\partial s^{\prime}}$$

量化误差的计算

在深度神经网络中，权重和激活值通常是32位浮点数，但这种高精度数据的存储和计算成本很高，因此需要将它们量化为更低比特位数的整数。LSQ量化采用了一种自适应的量化方法，即根据量化误差来动态调整量化参数，从而保证量化后的数据尽可能接近原始数据。

具体来说，假设原始数据为$x$，量化后的数据为$\hat{x}$，量化误差为$\Delta$，量化参数为$s$和$z$，则有以下公式：

$$\hat{x} = \text{round}(\frac{x}{s}) + z$$

$$\Delta = \text{max}(|x - (s\cdot\text{round}(\frac{x}{s}) + z)|)$$

其中，$\text{round}$表示四舍五入运算。上述公式的意义是，将原始数据$x$除以量化参数$s$并四舍五入，再乘以$s$加上偏置项$z$，得到量化后的数据$\hat{x}$。量化误差$\Delta$表示量化后的数据与原始数据之间的最大差值。量化参数$s$和$z$可以通过最小化量化误差来确定。

梯度的反向传播

LSQ量化对梯度的反向传播做了一些特殊处理，以保证梯度的正确性和有效性。具体来说，假设损失函数为$L$，权重参数为$w$，激活值为$a$，量化误差为$\Delta$，量化参数为$s$和$z$，则有以下公式：

$$\frac{\partial L}{\partial w} = \frac{\partial L}{\partial \hat{w}}\frac{\partial \hat{w}}{\partial w}$$

$$\frac{\partial L}{\partial a} = \frac{\partial L}{\partial \hat{a}}\frac{\partial \hat{a}}{\partial a}$$

其中，$\hat{w}$和$\hat{a}$表示量化后的权重和激活值，$\frac{\partial L}{\partial \hat{w}}$和$\frac{\partial L}{\partial \hat{a}}$表示损失函数对量化后的权重和激活值的梯度，$\frac{\partial \hat{w}}{\partial w}$和$\frac{\partial \hat{a}}{\partial a}$表示量化后的权重和激活值对原始权重和激活值的梯度。这些梯度可以通过误差反传算法计算得到。

需要注意的是，由于量化操作是不可导的，因此直接对量化后的数据求导是不可行的。LSQ量化采用了一种近似的梯度计算方法，即将量化误差$\Delta$作为损失函数的一部分，使得梯度的计算可以通过误差反传来实现。具体来说，可以将损失函数$L$表示为：

$$L = L_{\text{ori}} + \lambda\Delta$$

其中，$L_{\text{ori}}$表示原始的损失函数，$\lambda$为一个超参数，用于控制量化误差的影响。通过对$L$求关于$\hat{w}$和$\hat{a}$的梯度，可以得到：

$$\frac{\partial L}{\partial \hat{w}} = \frac{\partial L_{\text{ori}}}{\partial \hat{w}} + \lambda\frac{\partial \Delta}{\partial \hat{w}}$$

$$\frac{\partial L}{\partial \hat{a}} = \frac{\partial L_{\text{ori}}}{\partial \hat{a}} + \lambda\frac{\partial \Delta}{\partial \hat{a}}$$

其中，$\frac{\partial \Delta}{\partial \hat{w}}$和$\frac{\partial \Delta}{\partial \hat{a}}$可以通过误差反传计算得到。最终，可以通过$\frac{\partial L}{\partial w}$和$\frac{\partial L}{\partial a}$来更新原始的权重和激活值。

代码实现

下面是一个简单的LSQ量化代码实现，以量化权重为例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

import torch
import torch.nn as nn

class LSQQuantize(nn.Module):
    def __init__(self, nbits=8):
        super(LSQQuantize, self).__init__()
        self.nbits = nbits
        self.alpha = nn.Parameter(torch.Tensor([1.0]))
        self.zeta = nn.Parameter(torch.Tensor([0.0]))
        self.register_buffer('init_state', torch.Tensor([0]))
        self.register_buffer('prev_scale', torch.Tensor([0]))
        self.register_buffer('prev_zero_point', torch.Tensor([0]))
        self.reset_parameters()

    def reset_parameters(self):
        self.init_state.zero_()
        self.prev_scale.zero_()
        self.prev_zero_point.zero_()
        nn.init.uniform_(self.alpha, a=0.2, b=1.0)
        nn.init.zeros_(self.zeta)

    def forward(self, x):
        if self.training:
            # Compute the scale and zero point using moving average
            with torch.no_grad():
                x_abs = x.abs().flatten()
                k = int(x.numel() * 0.7)
                topk_val, _ = torch.topk(x_abs, k)
                scale = topk_val.mean() / (2 ** (self.nbits - 1) - 1)
                zero_point = torch.zeros_like(scale)
                self.prev_scale.mul_(0.99).add_(scale * 0.01)
                self.prev_zero_point.mul_(0.99).add_(zero_point * 0.01)

            # Quantize the weights using LSQ algorithm
            x_q = x / self.prev_scale
            x_q = x_q.clamp(-2 ** (self.nbits - 1), 2 ** (self.nbits - 1) - 1)
            x_q = torch.round(x_q)
            x_q = x_q * self.prev_scale

            # Update the scale and zero point using LSQ algorithm
            x_diff = (x - x_q).detach()
            x_diff_abs = x_diff.abs().flatten()
            x_diff_topk_val, _ = torch.topk(x_diff_abs, k)
            delta = x_diff_topk_val.mean()
            self.alpha.data = self.alpha.data - 0.01 * (self.alpha.data - (delta / (2 ** (self.nbits - 1) - 1))
        		self.zeta.data = self.zeta.data - 0.01 * (self.zeta.data - x_q.mean() / self.prev_scale)

            # Save the current state for next iteration
            self.init_state.fill_(1)
        else:
            # Quantize the weights using fixed scale and zero point
            x_q = x / self.prev_scale
            x_q = x_q.clamp(-2 ** (self.nbits - 1), 2 ** (self.nbits - 1) - 1)
            x_q = torch.round(x_q)
            x_q = x_q * self.prev_scale

        return x_q

上述代码实现了一个LSQ量化模块，可以将输入的权重$x$量化为$n$​比特整数。在训练阶段，LSQ量化模块会根据输入的数据动态调整量化参数$s$和$z$，并通过误差反传算法更新原始的权重，以保证量化后的数据尽可能接近原始数据。在推理阶段，LSQ量化模块会使用固定的量化参数$s$和$z$来量化输入的数据，以保证模型的稳定性。

LSQ相对一般量化训练

与传统的量化方法相比，LSQ量化具有以下优势：

1. 更好的量化精度：LSQ量化使用可学习的量化参数来代替固定的量化因子和量化函数，可以更好地适应不同的模型和数据分布，从而获得更好的量化精度。通过学习量化参数，LSQ量化可以优化量化误差，从而在保持模型精度的情况下，减少量化误差。

2. 更少的量化误差：传统的固定量化方法通常使用相同的量化因子和量化函数，无法适应不同的数据分布和模型结构，从而引入大量的量化误差。而LSQ量化使用可学习的量化参数，可以更好地适应不同的数据分布和模型结构，从而减少量化误差。

3. 更小的存储和计算开销：通过量化模型参数，可以将浮点数参数转换为整数，从而大大减少模型的存储和计算开销。而LSQ量化可以在保持模型精度的情况下，进一步减少量化误差，从而进一步减小模型的存储和计算开销。

4. 更好的通用性：LSQ量化可以适用于不同的深度学习模型和应用场景，可以在多种硬件平台上实现高效的推理和训练。LSQ量化可以与其他优化技术结合使用，如剪枝、权重共享和动态计算图等，从而实现更好的模型压缩和加速效果。

LSQ+

相对于LSQ，LSQ+的一个显著区别就是引入了非对称量化，把 0 也变成参数进行训练

$$\begin{aligned} & \bar{v}=\operatorname{round}\left(\operatorname{clip}\left((v-\beta) / s,-Q_N, Q_P\right)\right) \\ & \hat{v}=\bar{v} \times s+\beta \end{aligned}$$

结语

LSQ量化是一种基于梯度量化和误差反传的低比特量化方法，可以有效地减小深度神经网络的模型大小、加速推理速度并降低模型能耗。希望这篇博客对您有所帮助！

参考文献

• https://arxiv.org/pdf/2004.09576.pdf

• https://www.semanticscholar.org/paper/LSQ%2B%3A-Improving-low-bit-quantization-through-and-Bhalgat-Lee/8cc855854384755336aa05c5376ea455137bfbce

• https://www.cnblogs.com/jermmyhsu/p/16188288.html

• ← Previous Post
• Next Post →