Embedding Based Retrieval

向量召回，负样本的艺术!

Posted by Wang Junwei on 2022-03-01
向量召回｜Embedding Based Retrieval

最近越来越感觉到闷头写代码优化代码不是长久之计，一直在琢磨我们的算法同事在研究哪些方向，晓哥甩给我了这篇论文 EBR@Facebook，让我好好研究一下，Facebook是怎么做搜广推的。都说这篇文章是近几年最好的一篇向量召回算法领域的综述，我读完之后发现还是很不一样的，DR、TDM、YouTubeDNN、DSSM这些论文会大篇幅来介绍一种召回匹配模型，双塔的模型结构、模型的学习目标，损失函数等，这篇文章更像是方法论，一整篇都是Facebook（现在应该叫Meta了）怎样做EBR召回，样本设计tricks，ANN索引调参优化，端到端地优化整个系统，很有启发，浅浅的记录一下我的阅读心得。

搜索引擎overview

前言

互联网最早期的搜索引擎的代表是Google，建立在网页链接分析技术之上，用关键词对网页搜索，基于文本匹配的倒排索引，用关键词搜索网页，可以帮我们获取海量信息。但是基于文本匹配的搜索技术很难做到语义匹配（semantic matching）最近十年，深度学习在语音识别、机器视觉和自然语言理解中有了巨大的进步，基于Embedding的表示学习已经被证明是很有效果的手段。

通常来说，搜索引擎包括一个以低延迟和计算成本检索一组相关文档的召回层（recall layer），通常称为检索（Matching）也叫召回；以及一个使用更复杂的算法或模型将最需要的文档排在最前面的精确层（precision layer）， 通常称为排序（Ranking）也叫打分。

一般来说，电商搜索推荐引擎都包涵召回、海选、粗排、精排、重排和混排（如果有广告，值得一夸我司的搜推引擎都不区分自然商品和广告了😂）工程侧分为召回工程和打分工程（后者主要负责召回后链路的所有阶段的实时预估服务）

召回和打分的思路整体上就是互相对立的，召回要求粗、尽快从全量候选集中选出尽可能多的正确结果，打分要求细，从数千的候选集中筛选出几十个展现给用户，会用到特别复杂的模型和数以千计的特征，如下：

召回 打分
候选集 10亿+ 1000 ～ 5000
特征 少，一般抄的精排 多，会用到大量的交叉特征
模型 简单双塔、解耦 复杂DNN、交叉
时延要求 越快越多尽可能好 可以很慢要求精确

整个召回系统一般会有多路召回通道（包括文本召回、CF、ANN等），以ANN为主（其他召回通道为辅）互相补充：

  • 文本召回

    ​ 基于倒排文件索引、代表作是 ha3

  • 协同过滤

    ​ 基于协同过滤，i2i

  • 向量召回

    ​ 基于神经网络模型，ANN检索技术，代表作 Faiss

在merge去重之后进入海选打分。今天我们重点讨论一下向量召回（也就是ANN、或者EBR）

向量召回

向量召回是一种基于量空间模型的检索技术，它将文本、图像、音频等数据转化为向量表示，然后通过计算向量间的相似度，实现检索任务。在向量空间模型中，每个文档或者查询都被表示为一个向量，向量的每个维度对应一个特征，这些特征可以是词频、TF-IDF值、词向量等。

向量召回的核心思想是将文档或者查询映射到一个高维向量空间中，使得相似的文档或者查询在向量空间中距离较近，不相似的文档或者查询在向量空间中距离较远。这样，我们就可以通过计算向量之间的距离或者相似度，来实现检索任务。

Embedding技术 本质是将item / query的sparse 向量表征为 dense 向量的方式。

数学原理

向量空间模型是一种基于向量表示的文本检索模型，它将文档表示为向量，每个维度对应一个特征。在向量空间模型中，文档的相似度可以通过计算它们的向量之间的距离或者夹角余弦值来衡量。
sss

相似度计算

在向量空间模型中，我们可以使用多种相似度计算方法，包括余弦相似度、欧几里得距离、曼哈顿距离等。

  • 余弦相似度

余弦相似度是一种常用的相似度计算方法，它可以衡量两个向量之间的夹角余弦值，取值范围在[-1, 1]之间，值越大表示两个向量越相似。余弦相似度的计算公式如下：

cos⁡(θ)=a⃗⋅b⃗∣a⃗∣∣b⃗∣\cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}

其中，a⃗\vec{a}和b⃗\vec{b}分别表示两个向量，⋅\cdot表示向量的点积，∣a⃗∣|\vec{a}|和∣b⃗∣|\vec{b}|分别表示两个向量的模长。

  • 欧几里得距离

欧几里得距离是一种常用的距离计算方法，它可以衡量两个向量之间的欧几里得距离，即两个向之间的直线距离。欧几里得距离的计算公式如下：

d(a⃗,b⃗)=∑i=1n(ai−bi)2d(\vec{a}, \vec{b}) = \sqrt{\sum_{i=1}^{n}(a_i - b_i)^2}

其中，a⃗\vec{a}和b⃗\vec{b}分别表示两个向量，nn表示向量的维度。

  • 曼哈顿距离

曼顿距离是一种常用的距离计算方法，它可以衡量两个向量之间的曼哈顿距离，即两个向量之间的曼哈顿距离。曼哈顿距离的计算公式如下：

d(a⃗,b⃗)=∑i=1n∣ai−bi∣d(\vec{a}, \vec{b}) = \sum_{i=1}^{n}|a_i - b_i|

其中，a⃗\vec{a}和b⃗\vec{b}分别表示两个向量，nn向量的维度。

Embedding

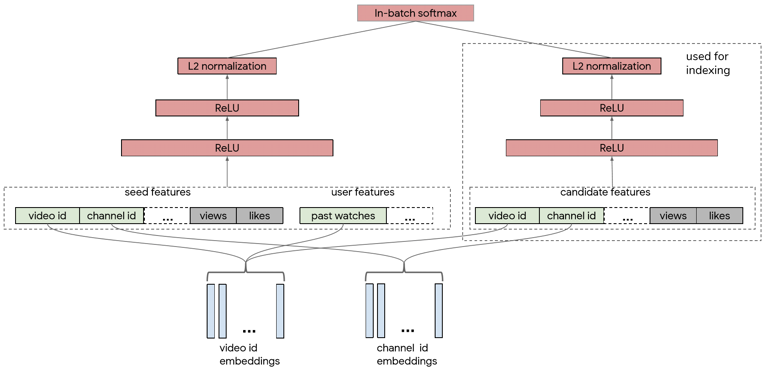
embedding的生成可以参考一下我的上一篇博客 🔗Embedding is all you need，经典方案有Word2Vec、DSSM、YoutubeDNN和BERT等，此处不再详述

双塔召回（Dual-Tower Vector Retrieva）

上文提到，召回模型需要解耦，与排序模型截然相反：排序模型十分鼓励特征交叉，候选集较少（比如我司精排入口1000个待打分商品）。召回需要面对全库候选集，亿级～10亿级的海量候选item，每个query和item都做交叉和DNN打分，那实时性要求是无论如何都无法保证的。

因此，双塔结构很自然的就被提出来了

User 塔和 item 塔天然分离，只在最后的点积计算时交叉，这样的好处：

  • offline

    item 和 user侧 embedding 独立，可以在user侧没有数据的时候，predict处所有item embedding

  • online

    user侧 embedding 可以独立打分获取，不需要item侧交叉，只需要过一遍user侧模型，打出user侧向量

img

图1.YouTubeDNN

EBR @Facebook

Embedding Based Retrieval in FaceBook Search

System Overview

EBR System

图2.Facebook EBR

Model

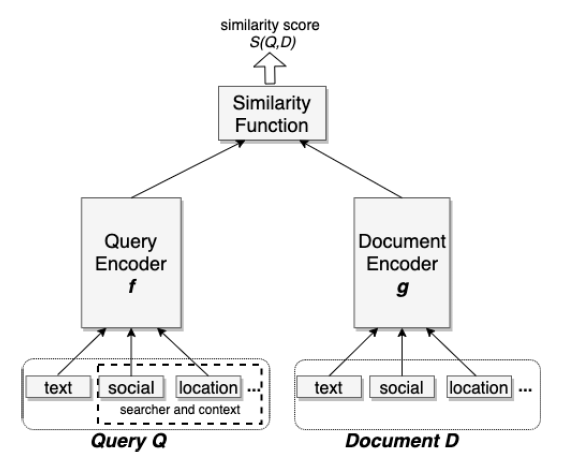
Facebook搜索EBR算法笔记

图3.EBR 双塔

将搜索检索任务制定为召回优化问题。 具体来说，给定一个搜索查询，其目标结果集 T={t1,t2,…,tN} ，以及模型返回的前 K 个结果

{d1,d2,…,dK} ，最终目标就是最大化前 K 个结果的召回率

recall@K=∑i=1Kdi∈TN.recall@K =\frac{\sum_{i=1}^K d_i \in T}{N}.

式子（4）recall@k是一个极其重要的指标，一般在离线阶段判断模型是否有效，可以看一下recall@topk就有初步的结论，然后再推到线上（A/B实验）

Loss Function

对给定的三元组 (q(i),d+(i),d−(i))\left(q^{(i)}, d_{+}^{(i)}, d_{-}^{(i)}\right), q(i)q^{(i)} 是输入, d+(i)d_{+}^{(i)} 和 d−(i)d_{-}^{(i)} 分别是正负样本， 三元损失为：

L=∑i=1Nmax⁡(0,D(q(i),d+(i))−D(q(i),d−(i))+m)L=\sum_{i=1}^N \max \left(0, D\left(q^{(i)}, d_{+}^{(i)}\right)-D\left(q^{(i)}, d_{-}^{(i)}\right)+m\right)

其中，D(u,v) 表示 u 和 v的相似度，m是一个超参数（enforced margin）是一个正负样本distance的阈值，来区分简单样本（easy example）

训练数据挖掘

排序是特征的艺术，召回是样本的艺术

如何定义负样本，是召回算法研究的核心问题，（BTW 我曾经努力追问一个即将上线的大项目LTR召回模型的样本策略，大佬说的很浅，只说了正负样本的比例，过于敏感的内容是算法的看家本领也不便告知）。

  • 正样本

    • 点击
    • 曝光

    实验结果显示在数据量相同的情况下，两者效果基本一致，即使是在曝光的正例基础上叠加点击正例，结果也没有进一步的提升。但是作者还是建议用曝光数据作为正样本，一是点击是用户主动行为，样本数量太少；二是未点击不意味着不好。

  • 负样本

    • 随机负样本
    • 曝光未点击 （粗排/精排的思路，未点击作为负样本）

    没想到的是，曝光未点积的负样本参与训练之后，召回率会显著下降55%（相比随机负样本），虽说召回模型的特征是从精排抄的，但是样本挖掘策略居然是不能直接拿过来用的。论文作者的解释为：这是因为这些负面因素偏向于可能在一个或多个因素中匹配查询的困难案例，而索引中的大多数文档都是简单的案例，根本不匹配查询。 将所有负例都设置为硬负例会改变训练数据对真实检索任务的代表性，这可能会对学习到的嵌入施加不小的偏差。

Features

论文里主要探讨了几个典型特征：

Text Feature

对于文本特征的构建，和之前word-n-gram 词袋模型不一样，EBR选用了 character-n-gram：

img

  • Word N-gram

    经典词袋模型

  • Character N-gram

    • 词汇量很有限（10万单词 --> 26 alphabet），Embedding Lookup table更小
    • **子词表示（subword representation）**对于我们在查询（例如拼写变体或错误）和文档方面（由于 Facebook 中的大量内容库存）遇到的词汇外问题具有鲁棒性。
Location Feature

位置匹配在许多搜索场景中都有优势，例如搜索本地企业/团体/事件。 为了让嵌入模型在生成输出嵌入时考虑位置，我们将位置特征添加到查询和文档端特征中。 对于查询端，我们提取了搜索者的城市、地区、国家和语言

Servings

serving用到的是ANN（Approximate Near Neighbor），针对高性能稠密向量的近似邻近检索，Facebook团队有自研的FAISS，支持HNSW、IVF、PQ、LSH、FLAT 和 GPU加速等加速手段。

这个是我的老本行，后面会有另外一篇博客详细介绍ANN检索算法和我在拼多多做的一系列优化，包括pack AB加速GEMM、GPU加速IVF、PQ量化还有INT4/8/16量化压缩等。

敬请期待！🫡

Later- Stage - Enhancement

搜索引擎全链路是一个很复杂多阶段的系统，每一层筛选漏斗都会逐步提炼筛选前面一层的结果。漏斗最底部的是向量召回，每一层的模型建模目标是为了优化当前层的效果，但是这一层出的品可能会被后链路漏斗（比如精排复杂模型）diss。为此：

  • 将召回候选的item embedding也一并召回，喂给精排模型，作为一个独立的特征；
  • 人工规则干预

Advanced Topics

篇幅有限，下一篇博客会详细介绍一下HNM，敬请期待。

Hard mining（难样本挖掘）
Embedding Ensemble

参考

FEATURED TAGS
FRIENDS