SICP Reading Notes

刚入大学的时候就听说过SICP这本书，大一开始断断续续地读了一些内容，当时没有系统性地总结也没有那么多的知识储备，大三下恰好疫情原因留在家中，又翻起了这本巨著，用博客记下自己的所思所得，与大家一起品读计算机代码里的灵魂。

这是我的读书笔记, 发布于我的主页: 汪俊威的博客

1. 背景

​ 《计算机程序的构造和解释》(Structure and Interpretation of Computer Programs，SICP)是一本关于计算机程序设计的总体性观念的基础教科书. 全书使用Lisp的Scheme方言来解释计算机科学的核心概念: 包括抽象，递归，解释器及元语言抽象，它由宏观到微观地给出计算机程序的轮廓与脉络.

​ SICP、CSAPP和TAOCP被誉为计算机科学的三大圣经，在MIT已经开设了近三十年的课程。

​

2. 构造过程抽象

计算机程序 = 过程 + 数据

• 数据 希望去操作的"东西"
• 过程 有关操作这些数据的规则的描述

2.1 过程抽象

​ 将过程抽象为函数, 方便复用和调用, 用Lisp的 define 具体实现:

• 递归 : 重复的调用函数(指本函数)实现自身函数调用循环

  1 2 3 4

  (define (fac n) (if (= n 1) 1 (* n (fac (- n 1)))))

  很明显, fac 函数就是一个阶乘运算. 具体运算如下:

  1 2 3 4 5 6 7 8 9 10

  (fac 5) (* 5 (fac 4)) (* 5 (* 4 (fac 3))) (* 5 (* 4 (* 3 (fac 2)))) (* 5 (* 4 (* 3 (* 2 (fac 1))))) (* 5 (* 4 (* 3 (* 2 1)))) (* 5 (* 4 (* 3 2))) (* 5 (* 4 6)) (* 5 24) 120

• 迭代: 函数内某段代码的重复循环.

  1 2 3 4 5 6 7 8

  (define (fac n) (define (iter product counter max-count) (if (> counter max-count) product (iter (* counter product) (+ counter 1) max-count))) (iter 1 1 n))

  这是fac函数的迭代函数, 具体运算如下:

  1 2 3 4 5 6 7 8

  (fac 5) (iter 1 1 5) (iter 1 2 5) (iter 2 3 5) (iter 6 4 5) (iter 24 5 5) (iter 120 6 5) 120

​

2.2 高阶函数抽象

​ 高阶函数抽象的基本思想: 将函数看作一等对象.

> - 在运行时创建
> - 能赋值给变量或数据结构中的元素
> - 能作为参数传给函数
> - 能作为函数的返回结果

如果面向对象式编程是用名词抽象世界，从而达到对于事物的封装和重用。

那函数式编程对应就是用动词抽象世界，从而达到对于行为的封装和重用。

• 在scheme中的体现

  知道程序语言的要求, 能为公共的模式命名, 建立抽象，而后直接在抽象的层次上操作.

  在scheme中允许将过程作为另一个过程的参数, 或者返回值来描述. 这是将过程(函数)视作一等对象.

  比如: 求和函数

  $$\sum_{n=a}^{b} f(n)=f(a)+\cdots+f(b)$$

  1 2 3 4 5

  (define (sum f a next b) (if (> a b) 0 (+ (f a) (sum f (next a) next b))))

• 高阶函数抽象: lambda表达式(匿名函数)

  C++	[](int a , int b) -> int { return a + b; }
  JAVA	(int x, int y) -> x + y ;
  Python	lambda x, y : x + y

  比如python的sorted() , 可以调用接口调整排序方式key =

  1 2	fruits = ['strawberry', 'fig', 'apple', 'cherry', 'raspberry', 'banana'] sorted(fruits, key=lambda word: word[::-1])

  高阶过程的重要性，在于使能显式地用程序设计语言的要素去描述这些抽象，使能像操作其他计算元素一样操作它们。如果了解过C++ , Java 或 python , 很容易看出函数式编程的高阶函数的普遍使用, 比如python的map, filter, reduce 和 apply

3. 构造数据抽象

计算机程序 = 过程 + 数据

• 数据 : 希望去操作的"东西"
• 过程 : 有关操作这些数据的规则的描述

3.1 数据抽象漫谈

​ 程序能表示自然世界的一些 场景, 物体 和 运转规则. 比如绝地求生的海岛地图世界, 比如手机左上角的时间日期. 比如高德导航的位置信息. 比如你正在阅读的博客. 需要用模型文件.obj 来存储3维信息; 需要用year-month-day的数据来表示日期, 需要用经度, 维度 和 海拔来表示具体位置信息. 等等这些都是寻求在程序里表达的大量事物, 但是他们大多数具有复合结构, 于是希望程序能以一种操作方式来操作多个数据的结合体. 将坐标的x,y和z作为一个单概念的元数据来操作.

​ 很显然, 数据抽象的特征类似于过程抽象, 不需要关注详细的实现过程, 只需要调用接口就可以了. 因为在创建过程抽象的时候, 函数如何实现的细节被隐蔽了.

​ 与之类似, 数据抽象是一种方法论，使将复合数据对象的使用细节与它的构造方式隔离.

​ 数据抽象的基本概念是构造操作抽象数据的程序。也就是说，的程序应该以一种方式来使用数据，对数据做出尽可能少的假设。同时，需要定义具体的数据表示，独立于使用数据的程序。系统中这两部分的接口是一系列函数，叫做选择器和构造器，它们基于具体表示实现了抽象数据。

3.2 数据结构抽象

​ 将数据组合起来, 形成复合数据. 构造数据抽象可以提升在设计程序时的概念层次, 提高设计的模块性.

• 隐藏起复合数据的实现细节
• 提供选择函数与构造函数作为接口，选择函数提取出复合数据内的更基本数据，构造函数提供组合起复合数据的方法
• 可以类比OO(object-oriented)语言的class理解数据抽象

3.2.1 序对

要实现数据抽象首先要有能把数据打成一个包的方法，叫它构造函数，还应该有能把数据从捆中取出来的方法，叫他选择函数。

在 Scheme 中提供了能实现这些方法的 API:

对于能非常方便构建 class 或是 struct 这样的数据结构的其他语言的使用者来看，这个序对的作用实在是微乎其微，但是大的抽象模式都是从最小的抽象方式开始的，这里使用序对也只是为了演示 Scheme 的抽象能力。

3.2.2 如何定义有理数

这看起来似乎不是个问题，因为语言都会原生支持各种类型的浮点数，能轻松的用来表示有理数，但是请先忘了有关这方面的知识，单纯考虑当的系统只能支持整形数据的时候应该怎么表示有理数。

从序对的知识出发，很容易找到答案，可以把有理数的小数点前后的部分，分别用一个整形数据来表示，再把他们用 cons 打包，当进行计算的时候再拆开计算就可以了。

所以对于有理数的定义甚至都可以用上面的函数来表示 ：

写实现也很简单 ：

1
2
3
4
5
6
7
8
9

; 直接打包
(define (make-rat x y) 
  (cons x y))
; 拿第一个数
(define (number bundle) 
  (car bundle))
; 拿第二个数
(define (number bundle)
  (cdr bundle))

这样就可以用上面的 API 去实现有理数的四则运算什么的 ：

1
2
3
4
5
6
7
8
9

(define (add-rat x y)
	(make-rat (+ (* (numer x) (denom y))
		(* (numer y) (denom x)))
		(* (denom x) (denom y))))
(define (sub-rat x y)
	(make-rat (- (* (numer x) (denom y))
		(* (numer y) (denom x)))
		(* (denom x) (denom y))))
; ... 还有很多

这样会发现 add-rat 、sub-rat 这样的函数作为过程抽象，仅接受定义的 有理数 类型 ( 即 cons 包裹的类型 ) 的数据就可以了，甚至完全不需要知道有理数到底是什么，只需要把有理数提交给过程，就可以拿到返回的有理数类型的返回结果了。

数据抽象和过程抽象相辅相承，在他们的帮助之下，为系统增加了类型，这无疑是一种新的进步，可以自己制作类型了。

3.2.3 实现抽象屏蔽

刚才的有理数程序可以体现为这样的一张层次图：

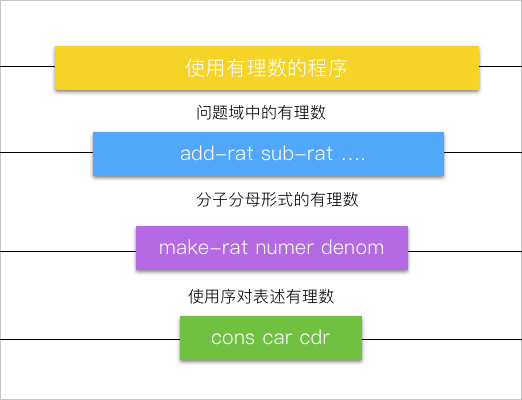
可以看出来，对于不同层次的程序来讲，有理数的意义都是不同的，对于使用的程序来讲，有理数就是一个普通元素，到了需要表示有理数的层次，有理数被分成了分子分母来使用，到了序对表述的层次，有理数是通过某种系统实现，将两个整形数据绑定在一起的。

实现这样的抽象屏障有什么好处？包括但不限于：

• 不同的部分关联极少，可以独立修改和增添方法。
• 修改实现方便，减少错误的发生。
• 修改方便的话，对设计就也有帮助，一些决策可以推迟。

Tips: 修改实现如何体现方便呢？

举个例子，如果换了实现 序对 的 API，那也只需要修改最下面一层就可以全部修改。相反，如果所有的方法都依赖于 最下层实现，比如如果的 add-rat 方法里面还是用了 car 、cdr 这样的方法，那如果想彻底改掉这套 API 需要修改下方全部的三层实现。

3.2.4 数据的过程实现

​ 之前使用的有理数程序，仅靠了三个基本过程去定义，而没有看到具体的实现过程，那么“数据到底是什么呢”？

​ 数据的抽象实现有很多种办法，这里挑一种不依赖低层实现，尽在 Scheme 中就能实现的方法，通过过程去实现数据抽象：

1
2
3
4
5
6
7
8
9

; cons 定义
(define (cons x y)
	(define (dispatch m)
		(cond ((= m 0) x)
			  ((= m 1) y)
			  (else (error "Argument error ")))))
; car / cdr 定义
(define (car z) (z 0))
(define (cdr z) (z 1))

当然 Scheme 中的数据实现肯定不是这么做的，为了效率很定是通过底层实现的。但是从这个例子里可以回顾在本书开头的一句话，过程和数据之间没有绝对界限，这里就看到了过程可以直接表示数据的能力。

Tips : Church encoding 丘奇计数

看起来很鬼畜，但是可以通过完全通过 lambda 演算去实现全部的整数运算系统。

比如说像下图一样，用 lambda 的层数去表达数字，还可以通过这个来实现运算。

4. 模块化、对象和状态

4.1 漫谈

​ 第二节和第三点 讲的是过程抽象和数据抽象, 但是对于一个更为拟真、更为复杂的系统的时候，以上或是计算、或是对模型抽象的知识就显得远远不足了。还应该需要一系列模式或者是说原则去规定去构建这整个系统。

​ 换句话说，要学习如何去模拟这个世界。

> 很多语言的设计者或是系统的实现者一直致力于让某种编程语言实现的系统去拟真现实世界，从中诞生了很多相关的思想和技术，OOP、OOC 还有各种设计模式都是这种努力的产出。另外很多语言也在致力于语法语义化，试图让编程语言 “看起来” 更像自然语言。

如何模拟世界

在学习很多 OOP 的语言的时候，都会讲很多 OOP 设计的好处，其中几个优点都有类似的特点，就是说 OOP 实际上是对现实世界的一种模拟，从开发人员的角度来说编写容易思考，而且从系统实现上也比较贴近现实。

在实现中可以从这两个角度去实现：

• 把现实中的每一种实体抽象为一个对应的程序对象（当然还可能会提取出对对象的抽象：类）
• 把每个现实中实现的具体方法模拟为一个程序中对应的活动。

通过对 “对象” 和 “活动” 的拟真，就可以用程序去对现实世界进行模拟。

遇到了一些问题

可以通过上面的两条去完成从现实到程序的一种转化。但是明显发现了一些问题，因为现实世界纷繁复杂，每时每刻的每个实体都在发生着不同的变化，而且每个实体都在发生着不同的动作，相互之间还有大量的交互，如果全部用程序去实现和模拟难以实现。

因而希望在程序在具体的实现之中，不要有大范围的甚至是全局的数据变化（这不好管理），希望把对象的增删修改、活动的产生消亡限定在一个有限的局部内。这样的整个系统会被分为不同的小的部分和结构，就把整个系统进行了分解的操作。

高内聚和低耦合

高内聚和低耦合是经常听到的设计方式，这样一个使用 模块化 的方式，其实是对这种设计思路的一种实践。高内聚是在说模块内聚化，功能内聚在对象之中，只留出相应的接口，使用接口进行交互，降低模块相互的耦合。

对象的世界

从 对象 的角度上来看，世界是什么样子的呢？对象的世界本质上是由一大堆对象组成的，对象有自己的属性和状态，随着时间的流逝，对象有一系列的状态的变迁。为此要通过一种方式去记录这个状态，通过这个被记录下的状态，能表现出这个对象的变化规程，而且还可以通过这个状态去继续计算对象的一系列后续的状态。

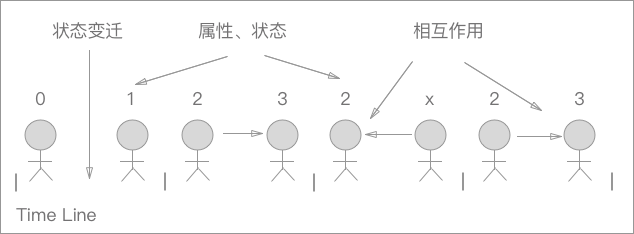
通过以上的这一系列的对 对象的世界 的描述，可以很容易的发现，描述的这种模块化、对象化的设计方式，其实和曾经学过的 Cpp、Java、CSharp 的世界非常的相近。从上帝的视角，把整个计算系统分解成对每个对象的计算的上去， 用它们模拟真实系统中对象的行为。

但是对上面提到的那个 状态的变化 会发现，缺少一个很熟悉的东西——赋值 ，下面对对象世界的展开讨论就要从 赋值 这个基本操作开始谈。

赋值和模块化

赋值 ，刚才怎么才想起来这个东西？回想起来之前两章所做的东西，所写的代码，似乎完全忘了赋值这件事（对 define 的使用和所谓赋值是不同的东西），使用了 代换原则 就搞定了所有的计算过程，所有的计算都可以被分解为基本数据和过程，根本就没有用上赋值，的世界也是闭环的。

但是此时潘多拉魔盒终于被打开，将引入赋值，昔日仅靠代换形成闭环的田园时代已经不复存在，邪恶的赋值为添加了新功能，也为带来了很多的麻烦。

局部状态

Tips 新的基本结构：

• begin

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

> ; begin 过程会对后面的所有表达式进行求值，然后返回最后一个表达式的值 > (begin <expr1> <expr2> <expr3>) > ``` > > * set! > ``` lisp > ; set! 是一种赋值操作，在 Scheme 中所有对数据进行修改的函数都会使用 ！ 尾缀 > ; 可以将一个值付给一个变量名称 > (set! <var> <value>) > ``` 如果仔细回想之前几节中写出的程序，似乎对它们的求值顺序并不在意（关于求值顺序在前文中提到过两种代换模型的方式：`应用序` 和 `正则序`），因为它是使用 `代换原则` 作为计算模型的程序，知道无论它按照什么顺序进行计算，最后都会被分解成基本的形式，所以本身的程序是没有时序关系的。 所以为什么说赋值破坏了这个模型呢？因为的值变成中途可变的了，在这个赋值的动作前后就形成了两个时间点，一个是赋值之前的状态，一个是赋值之后的状态，中途的数据变化会影响后续的求值过程，因而 `代换模型` 在这种情况下不再有效了。 上面说的是引入 `赋值` 要修复计算模型的问题，但是本身要让系统模块化还有着新的问题，刚才也谈到了要保留对象的历史进程，为了保留这个，就需要能控制一个对象的内部状态。 涉及到局部状态的内容，就会发现刚才提到的时序问题就很重要，比如说有一个银行账户，里面只有 100 元钱，提取一点就少一点，后续的提取一定是根据之前的提取的结果来继续提取，不能说这个东西没有时序，随意的提取。 需要的结果大概是这个样子的： ``` lisp (withdraw 20) 80 (withdraw 20) 60

如果根据直觉的话，可能会写出这样的代码：

1
2
3
4

; 写了一个生成 withdraw 的方法 还贴心的考虑到了 balance 作为局部变量传入，
; 用 lambda 来保存数据状态
(define (withdraw-generator balance)
  (lambda (amount) (- balance amount)))

这个方法看起来很不错，用到了之前学到的知识，使用类似这种 generator 的方法去返回一个过程，并且要维护局部变量么，用 lambda 来维护局部变量也是之前的知识点，不是很好么？

但是这个方法明显是不对的，实际运行起来只会看到这样的结果：

1
2
3
4
5

(define withdraw (withdraw-generator 100))
(withdraw 20)
80
(withdraw 20)
80

那么知道上文中的代码的一个显著的问题就是状态没办法随着时间的变化而继续的变化，那么利用 lambda 的闭包性所实现的状态保留也就没有意义了。

知道了问题所在在修改起代码的时候，就会轻松很多了，只要在每次计算完成的时候，用前面提到的 set! 方法去实现一次重新赋值就可以解决问题了：

1
2
3
4
5
6

(define (withdraw-generator balance)
  (lambda (amount)
          (if (>= balance amount)
              (begin (set! blance (- balance amount)) balance)
              "Insufficient funds")))
; 用 if 做了判断处理，并且使用了 begin 过程，在重新赋值之后返回了新值

在进行刚才的尝试就会发现程序和的预期的一样了：

1
2
3
4
5
6
7
8

(define withdraw1 (withdraw-generator 100))
(define withdraw2 (withdraw-generator 100))
(withdraw1 20)
80
(withdraw1 10)
70
(withdraw2 20)
80

并且使用两个变量去测试的时候能分得清这是两个对象，而不是同一段过程的反复调用，两个对象分别都有了自己的历史轨迹。

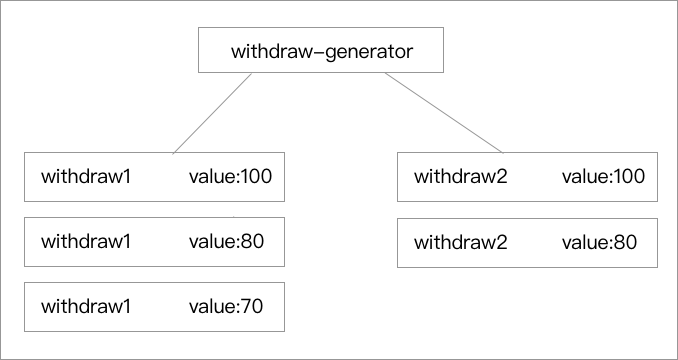
可以扩充一下这个方法，用到之前学到的 dispatch 方法，把这个方法写得更漂亮：

1
2
3
4
5
6
7
8
9
10
11
12

(define (make-account balance)
 (define (withdraw amount)
 (if (>= balance amount)
  (begin (set! balance (- balance amount)) balance)
  "Insufficient funds"))
 (define (deposit amount)
  (set! balance (+ balance amount)) balance)
 (define (dispatch m)
  (cond ((eq? m 'withdraw) withdraw)
  ((eq? m 'deposit) deposit)
  (else (error "Unknown req -- MAKE-ACCOUNT" m))))
dispatch)

通过这个方法可以通过方法名去使用这个银行账户：

1
2
3
4
5
6
7
8
9

(define acc (make-account 100))
((acc 'withdraw) 50)
50
((acc 'withdraw) 60)
"Insufficient funds"
((acc 'deposit) 40)
90
((acc 'withdraw) 60)
30

Tips define 和 set! 到底有什么区别：

define 和 set! 都能给一个变量赋值，但是 define 赋值只会定义当前环境内的约束，但是 set! 会考虑到环境的层级问题，并且还有就是 set! 赋值只能赋值一个特定的值，但是 define 的赋值对象则可以是一个 S 表达式。

这其中和环境赋值有关系的东西在后面还会讲到，这里只要简单记住区别就好。

赋值带来了？

一些好处

引入 赋值 自然是有他的好处的，从上面的例子很容易的看出通过使用 赋值 的方式保存了一个对象的状态，这就是系统实现模块化的根基。

可以再举一个例子去看出 状态 对有什么帮助，想写出一个反复调用都能生成具有统计性质均匀分布的随机序列，现在有 rand-update 这个方法（可求得随机序列的下一个值）了，应该怎么使用它呢？

1
2
3

; 伪代码
x2 = (rand-update x1)
x3 = (rand-update x2)

在手动的维护这样的一个随机序列的当前值，并且每次求出了之后都会再把这个当前值继续带入拿到下一个值，这么写就不如直接写一个维护当前值状态的生成函数：

1
2
3
4
5

(define rand
  (let ((x random-init))
   (lambda ()
	(set! x (rand-update x))
	 x)))

这样真的就省了很多的事情，并且从封装性上来看这也是一种进步，的随机数生成进化到一个能维持当前值的过程了。

另外如果还想说这种 命令式程序 的优势在哪，可能就是在表达状态和体现封装上，通过状态的记录，很轻松的就能实现一些具体的算法，代码可读性也比较的高，能清晰地反馈算法的本质，但是如果试图完全不用任何的状态记录（不使用任何的 赋值 语句），可能就要写很多的额外代码试图把状态通过参数的方式进行传递，书中通过一个蒙塔卡罗模拟 的例子介绍了这部分的知识，这里不再赘述。

同样多的代价

代价之前已经有过一些了解了，首先的之前在使用的 代换模型 没办法继续使用了。代换过程把表达式不断的化简到能把已有的约束带入，这样每个表达式的运算结果都是固定的，在这种框架之下没办法理解，为什么同样的一个过程运行两次，得到的结果是不同的。

为了理解这个问题，要理解在 代换模型 中，名字实际上只是一个约束、或者说是值的代号，因而才能通过代换消除名字进行计算（包含过程体）。但是在有赋值之后，名字和约束就不是一种能够进行等价替换的东西了，在这种情况下，名字更倾向把它理解成一种存储 值 的位置，或者说它是指向某一个存储 值 位置的一种指针，可以通过这个指针去访问、修改对应位置的一个 值 。但副作用就是指针不代表这个值，每次使用 值 的时候需要通过这个指针去访问。

在这种计算情况之下，变化的不只是赋值导致了简单计算模型的失效，这种变化还带来了更深远的影响，借由 “名字不再能表示一个值” 这个现实，开始思考程序中同一性的问题。

同一性产生了变化

说一种语言支持 同样的东西可以相互替换 ，而且这种替换不会改变表达式的值（程序的意义），称这种语言具有 引用透明性。在引入赋值之前，一直编写的程序都拥有 引用透明性。当引入赋值，程序失去程序的透明性之后，程序中对 “同一性” 的定义变得越来越复杂了。

赫拉克利特说：“人不可能两次踏进同一条河流”，这里对同一条的河流的定义就明显增加了对其中的河水的定义，因为河水一直在不断地流淌，参照引入赋值出现的对象的时间点问题，所以就不能认为这是一个同一条河流、同一个对象。

因而赋值打破了语言的 引用透明性：

• 同样东西 的概念不能通过形式化的描述直接确定
• 替换对程序的影响越来越难判定

来举一个例子来展示同一性产生的变化，比如 Paul 和 Peter 有银行账户，其中有 100 块钱。针对这种模拟有两种写法大家可以从这两种模拟的结果之中看出同一性变化带来的影响：

第一种模拟：

1
2

(define peter-acc (make-account 100))
(define paul-acc (make-account 100))

另一种模拟：

1
2

(define peter-acc (make-account 100))
(define paul-acc peter-acc)

Paul 和 Peter 在最开始使用的时候，都会发现自己的账户里面有 100 元钱，但是最后他们分别得提取或是充入钱，会让他们发现两种情况是不同的，在第一种模拟之下他们那使用的是不同的两个账户，但是在另一种模拟之下，他们使用的是同一个账户，但是在不具体使用之前，程序没有任何的表示这两个账户是共享和共通的。

Tips eq?

在很早的时候就接触过和同一性有关的东西，说过eq? 这个过程判断的是对象是否是同一的，而 equal? 检查的却是字面上的程序是否相等。

命令式程序的缺陷

会把基于 赋值 所构建的程序设计称为 命令式程序设计。基于命令式设计的程序由于无法使用代换模型，需要使用更为复杂的计算模型去解释，因而也很容易出现一些依赖时序性的问题。

举一个迭代式求阶乘过程的程序：

1
2
3
4
5
6

(define (factorial n)
  (define (iteritor product counter)
    (if	(> counter n)
        product
        (iteraotr (* counter product) (+ counter 1))))
  (iterator 1 1))

如果仍然用 Scheme 去实现这个求阶乘的过程，通过赋值去直接修改 prudect 和 counter 的数值，而不是使用参数传递：

1
2
3
4
5
6
7
8
9
10

(define (facatorial n)
  (let ((product 1)
        (counter 1))
       (define (iterator)
         (if (> counter n)
             product
             (begin (set! product (* counter product)) ; 用赋值代替传递参数
                    (set! counter (+ counter 1))
                    (iterator))))
       (iterator)))

但是这里面很明显的会发现，对 counter 的计算一定要放在 product 值计算的后面，如果这个顺序颠倒了的话，先更新了 counter 的计算，那依赖 counter 计算的 product 就会出现计算异常。

环境

在上一节中已经讨论过了，代换模型 不再适用，的 名字 不再是某个值的 别名 了，而是一个存储固定位置的指针，那就可以引入一种 环境模型 去解决一个问题，再很久以前的章节中，说过了 环境 本质上是一个存在与局部的表格（通常能通过各种 vector 和 map 去做具体实现），的 名字 和 值 存储于其中，通过对 名字 的访问、修改完成环境模型的调用。

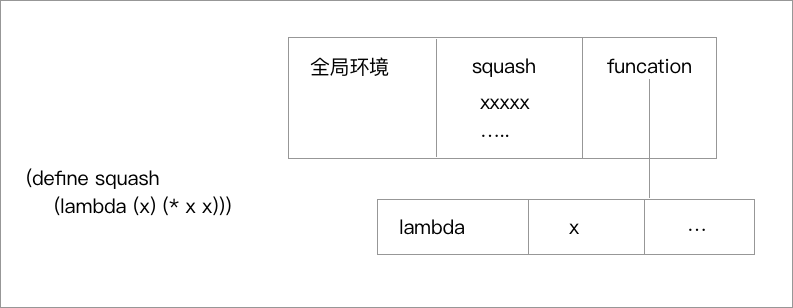
观察上图，的环境就是由层层的环境层次嵌套而得到的，针对每个内部环境都有一个环境，然后去指向挖补环境。由此可见，的环境非常重要，确定了新的求值模型的新的上下文条件，即使是之前写的代码也要依赖环境模型：

1

(+ 1 1)

即使是这样简单的数据相加，也要在环境中实现提供 加法+ 的具体实现才能进行正常的求值和计算。

Tips 解释器的构造

解释器的运行方式和环境模型有很大的关系，通过包含一个全局环境，再在运行时针对过程不断地创建新的环境并求值。

环境的求值

环境的求值规则变化也不是很大：

• 求出组合式各个子表达式的值
• 将运算符表达式的值赋给对象表达式的值
• 用 set! 和 define 修改和绑定环境约束
• 求值过程中环境逐渐变化

Tips 这里书中颇费笔墨的描述了很多个例子的具体的环境求值，我个人觉得这里只需要明白原理那些具体过程就好分析很多了。这里只举一个例子，从头到尾，从一个解释器的角度去看环境的求值模型到底是怎么回事。

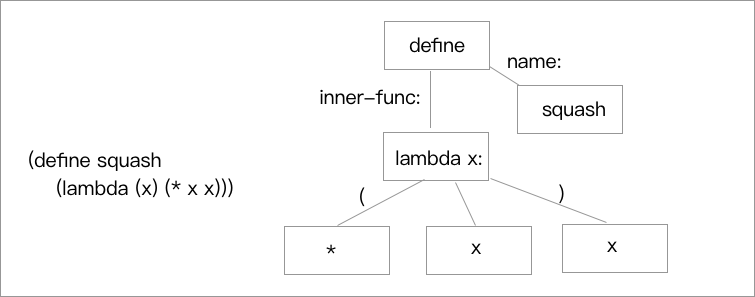
这里略过了词法分析，杜撰了一棵已经被整理好的 AST 树，假设有这么一个 解释器 针对这一个 AST 进行求值。

环境的绑定

首先的解释器接到了这棵 AST 树，然后从首层开始遍历去处理。

首先的解释器获取的是 define 节点和获取到它对应的 name ：squash，这时要进行的就是对本过程进行绑定。这时候就会在全局环境的 表格 之中插入一个对应项 squash，只需要给这个项目一个内部环境就可以啦，这个环境里不需要详细的对 lambda 部分进行展开，在其中保存好这个 AST 的结构就可以了，这样就可以在求值的时候，针对这个求值了。

绑定之后的场景就像是之前的图片一样

过程的应用

现在已经完成了过程在环境中的绑定问题，现在要在实际的运算中使用的这个过程，比如在过程中写出这样的代码：

1

(squash 5)

首先会创建一个新的求值环境，因为每次的程序调用都是一个独立的求值过程，因此可以在这个节点里面建立一个新的求值环境，新的环境的外围环境就是之前绑定的这个过程。

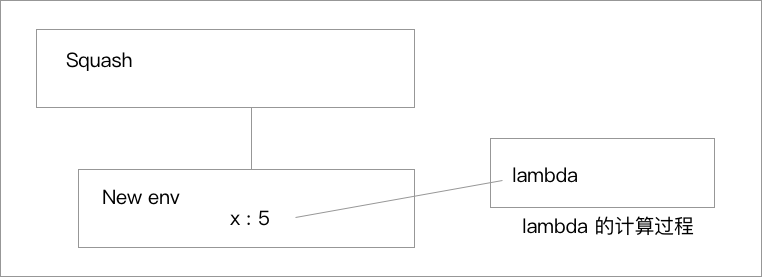
在新环境中要求值一个 lambda 表达式：

• 建立一个过程对象
• 其代码是该 lambda 表达式的过程体和参数
• 其环境指针指向 New env

Tips 再来看看 define 和 set! 的不同

• define 会添加当前框架的一个约束，而如果这个框架已经包含了这个约束的话，会对这个约束进行修改（参照具体的实现）
• set！会在当前环境里查找 的约束。如果当前框架里有，约束就确定了;否则到外围框架去找。查找可以沿外围环境指针前进多步，把找到的约束中变量的约束值修改为由 算出的值如果环境中没有<变量> 的约束(查找到达全局框架但仍未找到)，就报告变量无定义错误。

5. 元语言抽象

5.1 漫谈

在之前的篇幅之中讨论了很多和程序设计相关的内容，主要研究的三个内容是：

1. 数据抽象：如何组合程序的基本元素，构造更复杂的结构
2. 过程抽象：如何将复杂的结构抽象出高层组件，提供更高维度的组合型
3. 模块化，通过高抽象层次的组织方法，提高系统的模块性

通过这些手段已经足够设计大部分程序了，但是现实世界中遇到的问题可能更为复杂，或者可能类似的问题出现在同一个领域内。这时候可能就要在程序之中引入 DSL(领域内语言)了。本质上来讲引入 DSL 就是通过语言设计，为程序提供一种 语言层的抽象 ，来进一步提高程序的模块化。

5.2元语言抽象

这节之中会试着用 Scheme 来实现一个 Scheme 的解释器，用一种语言实现其自身的求值器，称为元循环（meta-circular）。这里可以复习一下 3.2 节之中出现的求值模型，其中的求值流程分成两步：

1. ‰求值组合式（非特殊形式）时
   • 先求值组合式的各子表达式
   • 把运算符子表达式的值作用于运算对象子表达式的值
2. ‰ 把复合过程应用于实参，是在一个新环境里求值过程体
   • 新环境：过程对象（里环境指针指向）的环境加一个新框架
   • 新框架里是过程的形参与对应实参的约束

这两个步骤构成了 Scheme 求值的基本循环，这两个步骤也是能相互调用和递归 (自己递归或相互递归。求值的子表达式可能要应用复合过程，过程体本身通常又是组合式)，逐步规约到：

• 符号 (从 env 里面取值）
• 基本过程（直接调用基本过程的代码）
• 值类型 (primary type 直接取值)

以上的两个步骤可以被抽象为过程 eval 和 apply ，其中 eval 负责表达式的求值，apply 把一个过程对象应用于一组实际参数，这两者相互递归调用，eval 还有自递归。eval 和 apply 就像下图的这个像是太极图一样的图里，两者相互调用相互生成。

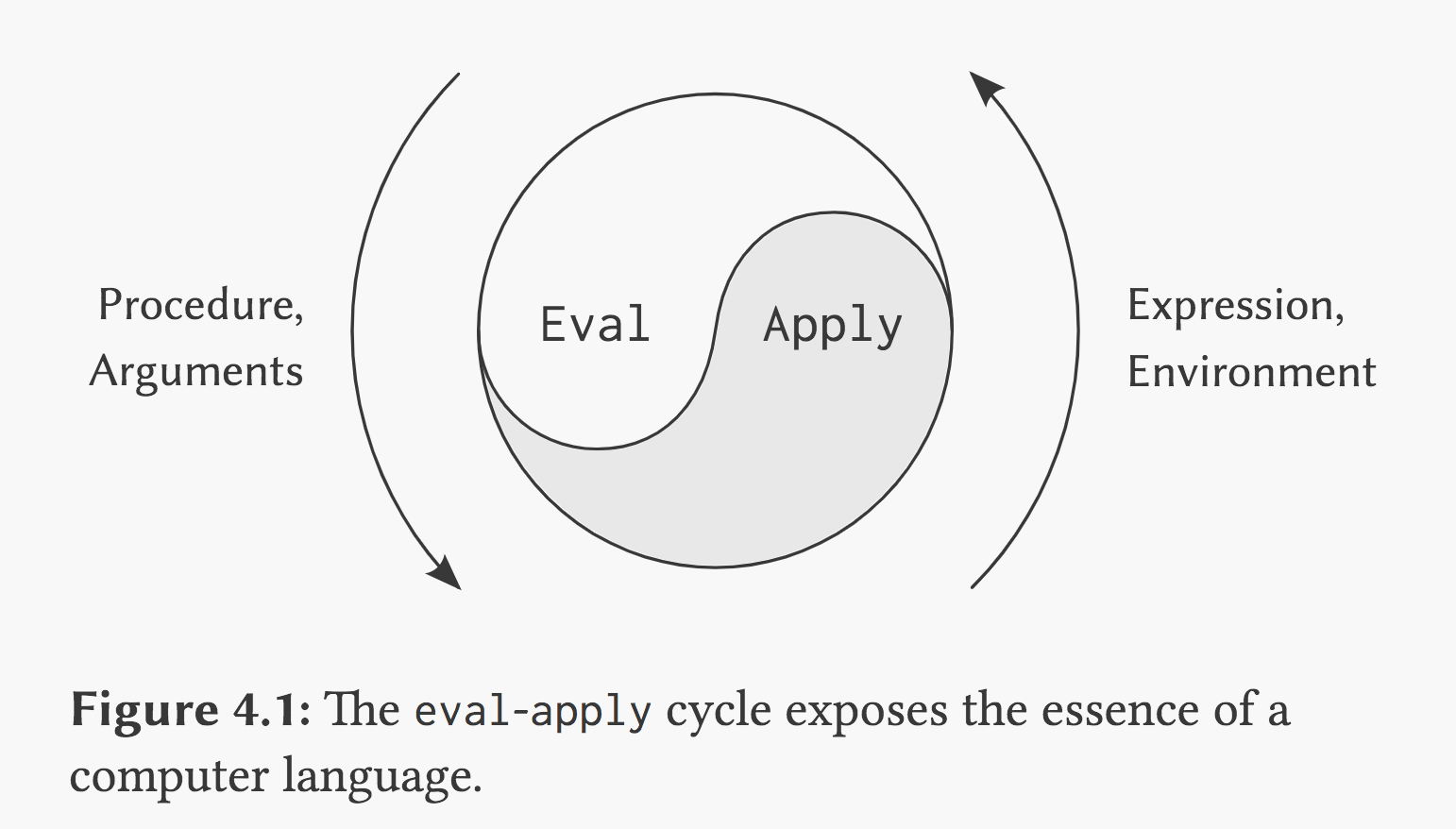
5.3 基础的递归解释器

5.4核心 eval 和 apply

整个 eval 和 apply 的过程直接看代码实现就可以了，这里可以看到 eval 的过程就是接受一个表达式 exp 和一个环境变量 env ，根据表达式类型的不同进行分别处理。

1
2
3
4
5
6
7
8

(define (eval exp env)
  (cond ((self-evaluating? exp) exp)                      ; 基本表达式
        ((variable? exp) (lookup-variable-value exp env)) ; 特殊形式
        ((quoted? exp) (text-of-quotation exp))
        ((assignment? exp) (eval-assignment exp env))
        ((definition? exp) (eval-definition exp env))
        ...                                               ; 组合形式
         (else (error "Unknown expression type: EVAL" exp))))

根据 exp 分情况来处理的过程，里面大概有三种类型的处理：

1. 基本表达式：包括能够自求值的表达式、变量
2. 各种特殊表达式：if、quote、lambda、cond 里面还会涉及到和 env 操作的部分
3. 过程结构：递归的对各个子表达式进行求值，然后 apply 应用过程

这里用 cond 写了一个 switch 结构的过程，这对处理的逻辑顺序有很多的要求，比如在一个 cond 的逻辑之中不同的分支的拜访位置不能有问题，不如使用数据分发的方式去设计这个 eval 的结构，还记得在第二章设计数据导向的 API 的时候做的事情么？首先是抽象一个 api 的表格：

1
2
3
4

; 操作／类型 ／过程
(put <op> <type> <item>)
; 操作／类型
(get <op> <type>)

然后给数据类型打上 tag 然后在使用前预先 install 对应的 api，这里甚至可以把不同类型的相同实现给出相同的名称，方便直接根据 data-type 去调用：

1
2
3
4
5
6
7
8
9
10

(define (install-rectangular-package)
; internal procedures
    (define (real-part z) (car z))
    (define (imag-part z) (cdr z))
  	; ... 省略其中的过程
    (put 'make-from-real-imag 'rectangular
        (lambda (x y) (tag (make-from-real-imag x y))))
    (put 'make-from-mag-ang 'rectangular
        (lambda (r a) (tag (make-from-mag-ang r a))))
'done)

不过暂时先不这么做，因为现在明显 eval 和 apply 的过程是混杂在一起，并没有对 expr 进行相应的预处理给每种数据结构打上 tag，这里可以看到 eval 和 apply 的互生带来了解释器设计和实现上的便利，但是也在具体的效率、代码编写的规范和拓展性上有了一定的问题。

接着来看核心的 apply 过程吧，apply 的应用过程就简单了很多，把 dispatch 放到比较具体的调用环境：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

(define (apply procedure arguments)
  (cond ((primitive-procedure? procedure) ; primary procedure
         (apply-primitive-procedure 
          procedure 
          arguments))
        ((compound-procedure? procedure)  ; compound procedure
         (eval-sequence
           (procedure-body procedure)
           (extend-environment
             (procedure-parameters 
              procedure)
             arguments
             (procedure-environment 
              procedure))))
        (else (error "Unknown procedure type: APPLY" procedure))))

1. primitive procedure 是 Scheme 里面也会出现的原生过程，这部分在 apply 的时候会直接下发给 Scheme 自带的 apply procedure ，因此在自己定义 apply 之前记得先保存下默认的实现。
2. compound-procedure 这个看起来也很简单，就是把各个 procedure 分别 eval 处理过之后又会回到 apply 过程之中，一个互生的调用又出现了。

####表达式处理和派生表达式

要是详细的介绍对各种表达式的处理过程未免失与琐碎，这里就只挑选一个有代表性的 if 语句来介绍处理过程，if 的具体 eval 实现过程如下：

1
2
3
4

(define (eval-if exp env)
  (if (true? (eval (if-predicate exp) env))
      (eval (if-consequent exp) env)
      (eval (if-alternative exp) env)))

这个过程非常的简单，其中的 if-predicate , if-consequent , if-alternative 都很不过是取出整个 if-expr 之中的不同部分的：

1
2
3
4
5
6
7

(define (if? exp) (tagged-list? exp 'if))
(define (if-predicate exp) (cadr exp))
(define (if-consequent exp) (caddr exp))
(define (if-alternative exp)
  (if (not (null? (cdddr exp)))
      (cadddr exp)
      'false))

整个 if 的流程就这样拆解完了，根据 predicate 拆借出来的结果运算流程重新进入了 eval 投入了其他表达式类型的求值过程之中。这里使用 if 作为例子还有一个因素就是这个 DSL 实现之中的 cond 语句没有自己的具体实现逻辑，而是依赖组合的 if 实现的，这被称作派生表达式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

(define (cond? exp) 
  (tagged-list? exp 'cond))
(define (cond-clauses exp) (cdr exp))
(define (cond-else-clause? clause)
  (eq? (cond-predicate clause) 'else))
(define (cond-predicate clause) 
  (car clause))
(define (cond-actions clause) 
  (cdr clause))
(define (cond->if exp)
  (expand-clauses (cond-clauses exp)))
(define (expand-clauses clauses)
  (if (null? clauses)
      'false     ; no else clause
      (let ((first (car clauses))
            (rest (cdr clauses)))
        (if (cond-else-clause? first)
            (if (null? rest)
                (sequence->exp 
                 (cond-actions first))
                (error "ELSE clause isn't 
                        last: COND->IF"
                       clauses))
            (make-if (cond-predicate first)
                     (sequence->exp 
                      (cond-actions first))
                     (expand-clauses 
                      rest))))))

上面这段代码比较核心的也就是 cond->if 相关的函数了，但是也非常的简单就是解析 cond 的结构，层层解析然后通过 make->if 生成逐级的 nested-if 。

解释器环境操作

解释器的运行环境和在第一章、第二章里面解释过的运行环境基本上是一个东西，这不过这里面要来手动实现这个环境。这里把环境理解为绑定参数的表格就好了。这里给出了环境提供的默认的几个 API：

1
2
3
4
5
6
7

(lookup-variable-value ⟨var⟩ ⟨env⟩)

(extend-environment ⟨variables⟩ ⟨values⟩ ⟨base-env⟩)

(define-variable! ⟨var⟩ ⟨value⟩ ⟨env⟩)

(set-variable-value! ⟨var⟩ ⟨value⟩ ⟨env⟩)

1. 其中的 lookup-variable-value 负责了在环境之中查找对应的变量，而 extend-environment 则是在根据上级环境来拓展新的 env。
2. define-variable! 和 set-variable-value! 这一对 API 就比较简单了在环境之中定义变量和修改变量。

Tips 基础递归解释器的 源码：

这里给出了基础的递归解释器的实现代码，这里的程序可以直接使用 racket 运行，记得要安装 sicp 的包。

PS：这里还有一个问题，就是之前提到要提前把 apply 方法保存起来，但是如果保存的过程和 apply 的定义同时出现在一个文件里，就会被 racket 认为是提前使用未定义方法 orz，因此这里单独把这个方法单独提出到一个文件里面引用了。

以数据作为程序

在上一节 基础的递归解释器 之中实现了一个用 Scheme 描述的 Scheme 解释器，意识到一个元循环解释器本质上也是一个 Scheme procedure 本身，只不过输入的内容变成了 Scheme 程序本身。这也就是本节标题的意味，以数据作为求值器的输入，因此能够把数据作为程序来使用。

举出一个非常熟悉的 factorial 过程：

1
2
3
4

(define (factorial n)
  (if (= n 1)
      1
      (* (factorial (- n 1)) n)))

如果把这个过程看做一台机器，那就获得了一台只能够计算斐波那契数的机器：

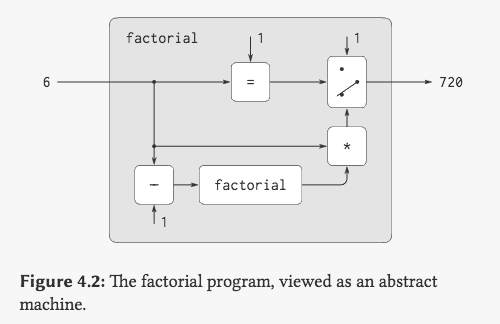
如果接受了这种设定，那就可以以更高维度的眼光来看上述的元循环求值器。如果 factorial 是一个特定的机器，那本身求值器就可以被认为是一台通用机器 (要素察觉)，其输入不再是一个具体的内容而是另一台机器（程序）的描述，而功能则变成了对这个机器的模拟过程。

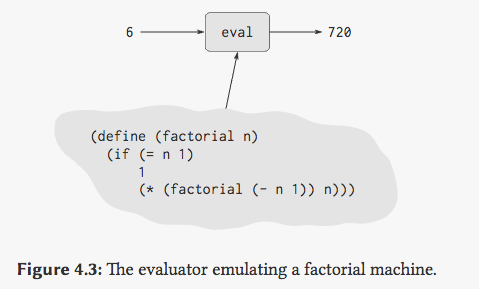
这里意识到，上面的描述 “另一台机器” 并不准确，求值器是 Scheme 的一个 procedure ，因此求值器本身也可以描述自己。这也就是在书中元循环解释器为什么会被描述为编程语言和用户之间的桥梁，因为用户的输入本身成为了程序运行的一部分，现代的大多数语言也大多都实现了应用内的 eval 过程。

其实在书中曾经提供以数据为程序的思想，当时的方式是把过程当成可传递的元素来处理，而现在能够提供更高层次的数据抽象 —— 抽象到语言。

图灵机

在上文中提到了求值器本质上是一个 "通用机器" ，这种描述方式让人感觉似曾相识。按照上文讨论的说法，通过 Scheme 本身实现了一个 Scheme 的解释器，忽略时间和空间的角度上来讲一个解释器可以模拟任意的其他解释器。这样原则上可计算的概念向揭示了一个有关 可计算性的 全新的领域，图灵根据上文的相似思想给出了称为图灵机的计算模型，证明了计算机的可实现。

图灵的基本思想是用机器来模拟人们用纸笔进行数学运算的过程，他把这样的过程看作下列两种简单的动作：

• 在纸上写上或擦除某个符号；
• 把注意力从纸的一个位置移动到另一个位置；

而在每个阶段，人要决定下一步的动作，依赖于（a）此人当前所关注的纸上某个位置的符号和（b）此人当前思维的状态。

为了模拟人的这种运算过程，图灵构造出一台假想的机器，该机器由以下几个部分组成：

1. 一条无限长的纸带TAPE。纸带被划分为一个接一个的小格子，每个格子上包含一个来自有限字母表的符号，字母表中有一个特殊的符号 ${\displaystyle \square } $ 表示空白。纸带上的格子从左到右依次被编号为0, 1, 2, …，纸带的右端可以无限伸展。
2. 一个读写头HEAD。该读写头可以在纸带上左右移动，它能读出当前所指的格子上的符号，并能改变当前格子上的符号。
3. 一套控制规则

TABLE

。它根据当前机器所处的状态以及当前读写头所指的格子上的符号来确定读写头下一步的动作，并改变状态寄存器的值，令机器进入一个新的状态，按照以下顺序告知图灵机命令：

1. 写入（替换）或擦除当前符号；
2. 移动 HEAD， ‘L’向左， ‘R’向右或者’N’不移动；
3. 保持当前状态或者转到另一状态
4. 一个状态寄存器。它用来保存图灵机当前所处的状态。图灵机的所有可能状态的数目是有限的，并且有一个特殊的状态，称为停机状态。

注意这个机器的每一部分都是有限的，但它有一个潜在的无限长的纸带，因此这种机器只是一个理想的设备。图灵认为这样的一台机器就能模拟人类所能进行的任何计算过程。图灵机这样的定义在现在看来是显然的，基本上就是一个 有限状态机的通俗化描述，但是在计算机还未诞生的当时代表了一种伟大的思想性革命。

结合上文，如果和使用的 Scheme 类比，每个 procedure 都能类比为一个特定的图灵机，那制作的 Scheme 解释器就可以类比于 元图灵机(Universal Turing-Machine) ，元图灵机以其他的图灵机作为输入能够模拟其他图灵机的行为，这也是为何说 通用机器 的描述不谋而合了。

Tips: 关于可计算性 (Computability)

关于图灵机、可计算性相关的知识笔者也只有概念上的理解。涉及到具体知识的学习笔者在看 CS121 Introduction to Theoretical Computer Science 这门入门课和 《Computability》这本书。

停机问题

在上一节图灵机的描述里面提到了图灵机有一个特殊的停机问题，通俗地说，停机问题就是判断任意一个程序是否能在有限的时间之内结束运行的问题。该问题等价于如下的判定问题：是否存在一个程序P，对于任意输入的程序w，能够判断w会在有限时间内结束或者死循环。这个题目也出现在了书中的 4.15 题目之中：

Exercise 4.15: Given a one-argument procedure p and an object a, p is said to “halt” on a if evaluating the expression (p a)returns a value (as opposed to terminating with an error message or running forever). Show that it is impossible to write a procedure halts? that correctly determines whether p halts on a for any procedure p and object a. Use the following reasoning: If you had such a procedure halts?, you could implement the following program:

1
2
3
4
5
6
7

(define (run-forever)
  (run-forever))

(define (try p)
  (if (halts? p p)
    (run-forever)
    'halted'))

这个 halts 肯定是找不到的，try 的实现本身就是 交叉 矛盾的，如果有 (halts? p p ) 为 True 那就会 run-forever 持续运行下去，而如果 (halts? p p) 为 False，那么程序又会 halted 。因此能非常直观的从程序而非逻辑、数学的角度来发现这个问题。

Tips 其实图灵发现的这个奇怪的反证方法并不是靠灵光一闪，而是康托尔 对角线方法 的一个实质的应用，读一下 《Gödel, Escher, Bach: An Eternal Golden Braid》 之中的相关章节，能获得更多的情报。

内部定义

内部定义这一节里主要讨论的问题的主要是关于查找环境引用，上面实现的 eval & apply 系统之中环境的置入都是按照顺序的，好在 Scheme 求值器的方法定义和实际使用的求值时机不同。例子可以看一下这个互调的方法示例：

1
2
3
4
5
6
7
8
9
10

(define (f x)
  (define (even? n)
    (if (= n 0)
        true
        (odd? (- n 1))))
  (define (odd? n)
    (if (= n 0)
        false
        (even? (- n 1))))
  ⟨rest of body of f⟩)

even 的过程被定义的时候 odd 的实现还没有被定义，按照定义的语义应该是 even 和 odd 同时被加入该环境。这在实际之中很难被实现，不过也应该能很简单的想出解决办法，可以在原部分放一个名字或者一个假的引用，当对应的 define 被填充进去了之后被调用就能正常被 link 到了。书中给出的方法其实也是其中的一种方法：

1
2
3
4
5
6
7
8
9
10
11
12

(lambda ⟨vars⟩
  (define u ⟨e1⟩)
  (define v ⟨e2⟩)
  ⟨e3⟩)

; 转换成
(lambda ⟨vars⟩
  (let ((u '*unassigned*)
        (v '*unassigned*))
    (set! u ⟨e1⟩)
    (set! v ⟨e2⟩)
    ⟨e3⟩))

这里是通过自动为每个定义块自动提前添加一个 let 的定义项目，然后先设置为预定义状态，然后当对应的项目被定义之后再对其进行重定.

6 总结

6.1 收获

   *  从另一个角度看程序和程序设计中的问题
   *  函数式程序设计
   *  多种多样的程序组织方式
   *  丰富多彩的编程模式
   *  对一些基础问题的理解

6.2 感想

如果笼统地概括SICP全书的主题，那么不外乎“抽象”二字。

还有一章没有读完, 希望暑假继续.

一起品读计算机代码里的灵魂。

• ← Previous Post
• Next Post →